Hostname: page-component-784d4fb959-nxbs6 Total loading time: 0 Render date: 2025-07-17T10:25:54.017Z Has data issue: false hasContentIssue false
  • English
  • Français

On the laws of the variety s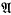e

Published online by Cambridge University Press:  09 April 2009

Roger M. Bryant
Roger M. Bryant
Affiliation:
Australian National UniversityCanberra
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A group is called an s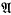-group if it is locally finite and all its Sylow subgroups are abelian. Kovács [4] has shown that, for any positive integer e, the class s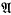e of all s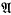-groups of exponent dividing e is a (locally finite) variety. The proof of this relies on the fact that, for any e, there are only finitely many (isomorphism classes of) non-abelian finite simple groups in s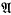e; and this is a consequence of deep results of Walter and others (see [6]). In [2], Christensen raised the finite basis question for the laws of the varieties s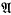e. It is easy to establish the finite basis property for an s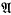e which contains no non-abelian finite simple group; and Christensen gave a finite basis for the laws of the variety s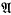30, whose only non-abelian finite simple group is PSL(2,5). Here we prove Theorem For any positive integer e, the varietys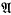ehas a finite basis for its laws.

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 14 , Issue 3 , November 1972 , pp. 364 - 367
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Roger, M. Bryant, ‘On locally finite varieties of groups’, Proc. London Math. Soc. (3) 24 (1972), 395–408.Google Scholar
[2]Christensen, C., ‘A basis for the laws of the variety s 30’, J. Austral. Math. Soc. 10 (1969), 493–496.CrossRefGoogle Scholar
[3]Huppert, B., Endliche Gruppen I (Springer-Verlag, Berlin, 1967).Google Scholar
[4]Kovács, L. G., ‘Varieties and finite groups’, J. Austral. Math. Soc. 10 (1969), 5–19.Google Scholar
[5]Neumann, Hanna, Varieties of Groups (Springer-Verlag, Berlin, 1967).CrossRefGoogle Scholar
[6]John, H. Walter, ‘The characterization of finite groups with abelian Sylow 2-subgroups’, Ann. of Math. 89 (1969), 405–514.Google Scholar