Article contents
ON THE BITS COUNTING FUNCTION OF REAL NUMBERS
Published online by Cambridge University Press: 01 August 2008
Abstract
Let Bn(x) denote the number of 1’s occurring in the binary expansion of an irrational number x>0. A difficult problem is to provide nontrivial lower bounds for Bn(x) for interesting numbers such as 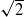 , e or π: their conjectural simple normality in base 2 is equivalent to Bn(x)∼n/2. In this article, amongst other things, we prove inequalities relating Bn(x+y), Bn(xy) and Bn(1/x) to Bn(x) and Bn(y) for any irrational numbers x,y>0, which we prove to be sharp up to a multiplicative constant. As a by-product, we provide an answer to a question raised by Bailey et al. (D. H. Bailey, J. M. Borwein, R. E. Crandall and C. Pomerance, ‘On the binary expansions of algebraic numbers’, J. Théor. Nombres Bordeaux16(3) (2004), 487–518) concerning the binary digits of the square of a series related to the Fibonacci sequence. We also obtain a slight refinement of the main theorem of the same article, which provides a nontrivial lower bound for Bn(α) for any real irrational algebraic number. We conclude the article with effective or conjectural lower bounds for Bn(x) when x is a transcendental number.
, e or π: their conjectural simple normality in base 2 is equivalent to Bn(x)∼n/2. In this article, amongst other things, we prove inequalities relating Bn(x+y), Bn(xy) and Bn(1/x) to Bn(x) and Bn(y) for any irrational numbers x,y>0, which we prove to be sharp up to a multiplicative constant. As a by-product, we provide an answer to a question raised by Bailey et al. (D. H. Bailey, J. M. Borwein, R. E. Crandall and C. Pomerance, ‘On the binary expansions of algebraic numbers’, J. Théor. Nombres Bordeaux16(3) (2004), 487–518) concerning the binary digits of the square of a series related to the Fibonacci sequence. We also obtain a slight refinement of the main theorem of the same article, which provides a nontrivial lower bound for Bn(α) for any real irrational algebraic number. We conclude the article with effective or conjectural lower bounds for Bn(x) when x is a transcendental number.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2008 Australian Mathematical Society
References
- 9
- Cited by

