No CrossRef data available.
Article contents
On certain direct sum decompositions of L1 spaces
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let L1 denote temporarily the usual Lebesgue space over the circle group (equivalently: the additive group of real numbers modulo 2π), and let H1 denote the Hardy space comprised of those f in L1 whose complex Fourier coefficients vanish for all negative frequencies, so tha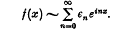 D. J. Newman has settled a conjecture by showing [1] that there exists no continuous projuction of L1 onto H1, i.e. that there exists in L1 no topological complement to H1.
D. J. Newman has settled a conjecture by showing [1] that there exists no continuous projuction of L1 onto H1, i.e. that there exists in L1 no topological complement to H1.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1963
References
[1]Newman, D. J., The non-existence of projections from L1 to H1, Proc. Amer. Math. Soc. 12 (1961), 98–99.Google Scholar
[3]Weil, A., L'intégration dans les groupes topologiques et ses applications, Act. Sci. et Ind. Nc. 869–1145, Paris (1951).Google Scholar
[4]Hewitt, E. and Zuckerman, H. S., Some theorems on lacunary Fourier series, with extensions to compact groups, Trans. Amer. Math. Soc. 93 (1959). 1–19.CrossRefGoogle Scholar
[5]Rudin, W., Trigonometric series with gaps, Journ. Math. and Mech. 9 (1960), 203–228.Google Scholar

