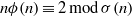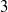Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bujačić, Sanda
2017.
A variation of a congruence of Subbarao for
$$n=2^{\alpha }5^{\beta }$$
n
=
2
α
5
β
.
Periodica Mathematica Hungarica,
Vol. 75,
Issue. 1,
p.
66.