Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vsemirnov, M.
2004.
Hurwitz Groups of Intermediate Rank.
LMS Journal of Computation and Mathematics,
Vol. 7,
Issue. ,
p.
300.
Tamburini, M.C.
and
Vsemirnov, M.
2006.
Vol. 4,
Issue. ,
p.
385.

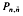 of
of 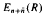 consisting of the matrices of shape
consisting of the matrices of shape 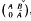 , where
, where 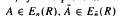 and
and 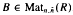 , is (2, 3, 7)-generated whenever
, is (2, 3, 7)-generated whenever 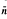 are large enough.
are large enough.