No CrossRef data available.
Article contents
Omitted rays and wedges of fractional Cauchy transforms
Part of:
Miscellaneous topics of analysis in the complex domain
Spaces and algebras of analytic functions
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For α > 0 let 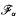 α denote the set of functions which can be expressed
α denote the set of functions which can be expressed 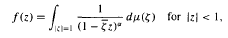 where μ is a complex-valued Borel measure on the unit circle. We show that if f is an analytic function in Δ = {z ∈
where μ is a complex-valued Borel measure on the unit circle. We show that if f is an analytic function in Δ = {z ∈ 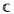 : |z| < 1} and there are two nonparallel rays in
: |z| < 1} and there are two nonparallel rays in 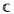 /f(Δ) which do not meet, then f ∈
/f(Δ) which do not meet, then f ∈ 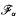 α where απ denotes the largest of the two angles determined by the rays. Also if the range of a function analytic in Δ is contained in an angular wedge of opening απ and 1 < α < 2, then f ∈
α where απ denotes the largest of the two angles determined by the rays. Also if the range of a function analytic in Δ is contained in an angular wedge of opening απ and 1 < α < 2, then f ∈ 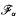 α.
α.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2006
References
[1]Bourdon, P. and Cima, J. A. ‘On integrals of Cauchy-Stieltjes type’, Houston J. Math. 14 (1988), 465–474.Google Scholar
[2]Havin, V. P. ‘On analytic functions representable by an integral of Cauchy-Stieltijes type’, Vestnik Leningrad Univ. Ser. Mat. Meh. Astronom. 13 (1958), 66–79 (in Russian).Google Scholar
[3]Hibschweiler, R. A. and MacGregor, T. H., ‘Closure properties of families of Cauchy-Stieltjes transforms’, Proc. Amer. Math. Soc. 105 (1989), 615–621.CrossRefGoogle Scholar
[4]Hibschweiler, R. A. and MacGregor, T. H. ‘Multipliers of families of Cauchy-Stieltjes transforms’, Trans. Amer. Math. Soc. 331 (1992), 377–394.CrossRefGoogle Scholar
[5]MacGregor, T. H. ‘Analytic and univalent functions with integral representations involving complex measures’, Indiana Univ. Math. J. 36 (1987), 109–130.CrossRefGoogle Scholar
[6]MacGregor, T. H. ‘Fractional Cauchy transforms’, J. Comput. Appl. Math. 105 (1999), 93–108.CrossRefGoogle Scholar

