Article contents
A note on centre-by-finite-exponent varieties of groups
Published online by Cambridge University Press: 09 April 2009
Extract
We refer the reader to Hanna Neumann [7] for notation and other undefined terms. Let 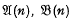 and
and 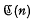 denote the varieties of groups defined by the laws (xy)n=xnyn, [x, y]n=1 and [x, yn]respectively, where n is an integer.
denote the varieties of groups defined by the laws (xy)n=xnyn, [x, y]n=1 and [x, yn]respectively, where n is an integer. 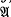 (n)-groups were termed “n-abelian” by R. Baer [1] and have been a subject matter of investigation by various authors (see [3], [5], [6] and the references therein). Recently KaluŽnin [5] has shown that
(n)-groups were termed “n-abelian” by R. Baer [1] and have been a subject matter of investigation by various authors (see [3], [5], [6] and the references therein). Recently KaluŽnin [5] has shown that 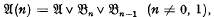 , thus clarifying the relationship between U(n) and the familiar varieties. From the elementary inequalities
, thus clarifying the relationship between U(n) and the familiar varieties. From the elementary inequalities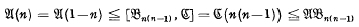 (n ≠ 0,1)it is easily deduced that
(n ≠ 0,1)it is easily deduced that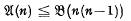 (see for instance [5]). If G = Cm Wr C∞, then cleary
(see for instance [5]). If G = Cm Wr C∞, then cleary 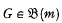 but
but 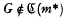 for any
for any 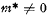 Thus
Thus 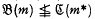 and
and 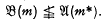 . It is also easy to see that in general
. It is also easy to see that in general 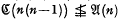 (see for instance [6] § 5.1) and we are led to ask
(see for instance [6] § 5.1) and we are led to ask
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1970
References
- 7
- Cited by

