Article contents
LIMITS OF FRACTIONAL DERIVATIVES AND COMPOSITIONS OF ANALYTIC FUNCTIONS
Published online by Cambridge University Press: 28 September 2016
Abstract
Suppose that the function 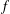 $f$ is analytic in the open unit disk
$f$ is analytic in the open unit disk 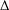 $\unicode[STIX]{x1D6E5}$ in the complex plane. For each
$\unicode[STIX]{x1D6E5}$ in the complex plane. For each 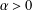 $\unicode[STIX]{x1D6FC}>0$ a function
$\unicode[STIX]{x1D6FC}>0$ a function 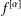 $f^{[\unicode[STIX]{x1D6FC}]}$ is defined as the Hadamard product of
$f^{[\unicode[STIX]{x1D6FC}]}$ is defined as the Hadamard product of 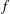 $f$ with a certain power function. The function
$f$ with a certain power function. The function 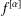 $f^{[\unicode[STIX]{x1D6FC}]}$ compares with the fractional derivative of
$f^{[\unicode[STIX]{x1D6FC}]}$ compares with the fractional derivative of 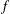 $f$ of order
$f$ of order  $\unicode[STIX]{x1D6FC}$ . Suppose that
$\unicode[STIX]{x1D6FC}$ . Suppose that 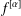 $f^{[\unicode[STIX]{x1D6FC}]}$ has a limit at some point
$f^{[\unicode[STIX]{x1D6FC}]}$ has a limit at some point 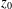 $z_{0}$ on the boundary of
$z_{0}$ on the boundary of 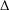 $\unicode[STIX]{x1D6E5}$ . Then
$\unicode[STIX]{x1D6E5}$ . Then 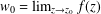 $w_{0}=\lim _{z\rightarrow z_{0}}f(z)$ exists. Suppose that
$w_{0}=\lim _{z\rightarrow z_{0}}f(z)$ exists. Suppose that 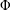 $\unicode[STIX]{x1D6F7}$ is analytic in
$\unicode[STIX]{x1D6F7}$ is analytic in 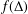 $f(\unicode[STIX]{x1D6E5})$ and at
$f(\unicode[STIX]{x1D6E5})$ and at 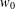 $w_{0}$ . We show that if
$w_{0}$ . We show that if 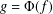 $g=\unicode[STIX]{x1D6F7}(f)$ then
$g=\unicode[STIX]{x1D6F7}(f)$ then 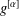 $g^{[\unicode[STIX]{x1D6FC}]}$ has a limit at
$g^{[\unicode[STIX]{x1D6FC}]}$ has a limit at  $z_{0}$ .
$z_{0}$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

