No CrossRef data available.
Article contents
LANDAU’S THEOREM, FIELDS OF VALUES FOR CHARACTERS, AND SOLVABLE GROUPS
Published online by Cambridge University Press: 23 December 2016
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
When 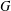 $G$ is a finite solvable group, we prove that
$G$ is a finite solvable group, we prove that 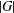 $|G|$ can be bounded by a function in the number of irreducible characters with values in fields where
$|G|$ can be bounded by a function in the number of irreducible characters with values in fields where 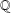 $\mathbb{Q}$ is extended by prime power roots of unity. This gives a character theory analog for solvable groups of a theorem of Héthelyi and Külshammer that bounds the order of a finite group in terms of the number of conjugacy classes of elements of prime power order. In particular, we obtain for solvable groups a generalization of Landau’s theorem.
$\mathbb{Q}$ is extended by prime power roots of unity. This gives a character theory analog for solvable groups of a theorem of Héthelyi and Külshammer that bounds the order of a finite group in terms of the number of conjugacy classes of elements of prime power order. In particular, we obtain for solvable groups a generalization of Landau’s theorem.
Information
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
Gajendragadkar, D., ‘A characteristic class of characters of finite p-separable groups’, J. Algebra
59(2) (1979), 237–259.CrossRefGoogle Scholar
Héthelyi, L. and Külshammer, B., ‘Elements of prime power order and their conjugacy classes in finite groups’, J. Aust. Math. Soc.
78(2) (2005), 291–295.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, San Diego, CA, 1976).Google Scholar
Isaacs, I. M., ‘Abelian normal subgroups of M-groups’, Math. Z.
182(2) (1983), 205–221.CrossRefGoogle Scholar
Isaacs, I. M., ‘Characters of 𝜋-separable groups’, J. Algebra
86(1) (1984), 98–128.CrossRefGoogle Scholar
Isaacs, I. M., ‘Characters of solvable groups’, in: The Arcata Conference on Representations of Finite Groups (Arcata, CA, 1986), Proceedings of Symposia in Pure Mathematics, 47, Part 1 (American Mathematical Society, Providence, RI, 1987), 103–109.CrossRefGoogle Scholar
Isaacs, I. M., ‘Characters and Hall subgroups of groups of odd order’, J. Algebra
157(2) (1993), 548–561.CrossRefGoogle Scholar
Isaacs, I. M., ‘The 𝜋-character theory of solvable groups’, J. Aust. Math. Soc. Ser. A
57(1) (1994), 81–102.CrossRefGoogle Scholar
Landau, E., ‘Über die Klassenzahl der binären quadratischen Formen von negativer Discriminante’, Math. Ann.
56(4) (1903), 671–676.CrossRefGoogle Scholar
Lewis, M. L., ‘
 $B_{\unicode[STIX]{x1D70B}}$
-characters and quotients’, 2016. arXiv:1609.02029.Google Scholar
$B_{\unicode[STIX]{x1D70B}}$
-characters and quotients’, 2016. arXiv:1609.02029.Google Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar

