Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Chang-Pao
1987.
Pointwise Convergence of Trigonometric Series.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 43,
Issue. 3,
p.
291.
Móricz, Ferenc
1989.
OnL 1-convergence of Walsh-Fourier series I.
Rendiconti del Circolo Matematico di Palermo,
Vol. 38,
Issue. 3,
p.
411.
Móricz, Ferenc
1991.
On the integrability and 𝐿¹-convergence of complex trigonometric series.
Proceedings of the American Mathematical Society,
Vol. 113,
Issue. 1,
p.
53.
Móricz, Ferenc
1994.
L 1-convergence of double cosine- and Walsh-Fourier series.
Journal d'Analyse Mathématique,
Vol. 62,
Issue. 1,
p.
115.
Giang, Dᾰng Vũ
and
Móricz, Ferenc
1996.
On the L1-convergence of Fourier transforms.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 60,
Issue. 3,
p.
405.
Chen, Chong Hu
1996.
Group Theory in China.
p.
1.
Zaderei, P. V.
and
Smal', B. A.
2002.
On the Convergence of Fourier Series in the Space L1.
Ukrainian Mathematical Journal,
Vol. 54,
Issue. 5,
p.
785.
Kaur, Kulwinder
Bhatia, S. S.
and
Ram, Babu
2003.
L 1-convergence of complex double fourier series.
Proceedings Mathematical Sciences,
Vol. 113,
Issue. 4,
p.
355.

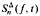 and establish its
and establish its 