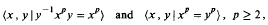Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brazil, Marcus
1994.
Growth functions for some nonautomatic Baumslag-Solitar groups.
Transactions of the American Mathematical Society,
Vol. 342,
Issue. 1,
p.
137.
Chiswell, I. M.
1994.
The growth series of HNN extensions.
Communications in Algebra,
Vol. 22,
Issue. 8,
p.
2969.
Collins, D. J.
Edjvet, M.
and
Gill, C. P.
1994.
Growth series for the group ?x,y�x ?1 yx=y l ?.
Archiv der Mathematik,
Vol. 62,
Issue. 1,
p.
1.
Brazil, Marcus
1995.
Computational Algebra and Number Theory.
p.
1.
Grigorchuk, R.
and
De La Harpe, P.
1997.
On problems related to growth, entropy, and spectrum in group theory.
Journal of Dynamical and Control Systems,
Vol. 3,
Issue. 1,
p.
51.
GILL, C. P.
1999.
GROWTH SERIES OF STEM PRODUCTS OF CYCLIC GROUPS.
International Journal of Algebra and Computation,
Vol. 09,
Issue. 01,
p.
1.
Freden, Eric M.
Knudson, Teresa
and
Schofield, Jennifer
2011.
Growth in Baumslag–Solitar groups I: subgroups and rationality.
LMS Journal of Computation and Mathematics,
Vol. 14,
Issue. ,
p.
34.
Burillo, José
and
Elder, Murray
2015.
Metric properties of Baumslag–Solitar groups.
International Journal of Algebra and Computation,
Vol. 25,
Issue. 05,
p.
799.
Sánchez, Ayla P.
and
Shapiro, Michael
2018.
Growth in higher Baumslag–Solitar groups.
Geometriae Dedicata,
Vol. 195,
Issue. 1,
p.
79.
Karpuz, Eylem Güzel
and
Çetinalp, Esra Kirmizi
2018.
Growth series of crossed and two-sided crossed products of cyclic groups.
Mathematica Slovaca,
Vol. 68,
Issue. 3,
p.
537.
Dudkin, F.A.
2020.
$$\mathcal {F}_\pi $$-residuality of generalized Baumslag–Solitar groups.
Archiv der Mathematik,
Vol. 114,
Issue. 2,
p.
129.
Adams, Jared
and
Freden, Eric M.
2020.
Growth in Baumslag–Solitar groups II: The Bass–Serre tree.
International Journal of Algebra and Computation,
Vol. 30,
Issue. 02,
p.
339.