No CrossRef data available.
Article contents
A generalization of the Hall semigroup of a band
Part of:
Semigroups
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let E be a band and ε a compatible partition on it. If S is an orthodox semigroup with band of idempotents E such that there exists a congruence on S inducing the partition ε then we define a homomorphism of S into a Hall semigroup whose kernel is the greatest congruence on S inducing the partition ε. On the other hand, we define a subsemigroup 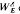 of the Hall semigroup WE possessing the property that S is an othodox semigroup with band of idempotents E which has a congruence inducing ε if and only if the range of the Hall homomoprhism of S into WE is contained in
of the Hall semigroup WE possessing the property that S is an othodox semigroup with band of idempotents E which has a congruence inducing ε if and only if the range of the Hall homomoprhism of S into WE is contained in 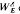 .
.
MSC classification
Secondary:
20M10: General structure theory
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1980
References
Clifford, A. H. and Preston, G. B. (1961, 1967), The algebraic theory of semigroups. Volumes I, II (Math. Surveys 7, Amer. Math. Soc., Providence, R.I.).Google Scholar
Feigenbaum, R. (1976), ‘Kernels of orthodox semigroup homomorphisms’, J. Austral. Math. Soc. 22, 234–245.CrossRefGoogle Scholar
Howie, J. M. (1976), An introduction to semigroup theory (Academic Press, London, New York, San Francisco).Google Scholar
Meakin, J. (1970), ‘Idempotent-equivalent congruences on orthodox semigroups’, J. Austal. Math. Soc. 11, 221–241.CrossRefGoogle Scholar
Reilly, N. R. and Scheiblich, H. E. (1967), ‘Congruences on regular semigroups’, Pacific J. Math. 23, 349–360.CrossRefGoogle Scholar

