No CrossRef data available.
Article contents
EVALUATION FUNCTIONS AND REFLEXIVITY OF BANACH SPACES OF HOLOMORPHIC FUNCTIONS
Part of:
Linear function spaces and their duals
Topological linear spaces and related structures
Analytic spaces
Published online by Cambridge University Press: 31 May 2024
Abstract
Let 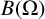 $B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain
$B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain  $\Omega $ in
$\Omega $ in 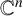 ${{\mathbb C}^n}$. In this paper, we establish a criterion for
${{\mathbb C}^n}$. In this paper, we establish a criterion for 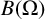 $B(\Omega )$ to be reflexive via evaluation functions on
$B(\Omega )$ to be reflexive via evaluation functions on 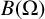 $B(\Omega )$, that is,
$B(\Omega )$, that is, 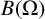 $B(\Omega )$ is reflexive if and only if the evaluation functions span the dual space
$B(\Omega )$ is reflexive if and only if the evaluation functions span the dual space 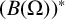 $(B(\Omega ))^{*} $.
$(B(\Omega ))^{*} $.
MSC classification
Primary:
32C37: Duality theorems
46A25: Reflexivity and semi-reflexivity
46E15: Banach spaces of continuous, differentiable or analytic functions
Secondary:
46A20: Duality theory
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by NNSF of China (Grant Number 12071155). The second author was supported by NNSF of China (Grant Number 12371127). The third author is supported by the Australian Research Council (ARC) through the research grant DP220100285.
Communicated by Lisa Orloff Clark
References
Conway, J. B., A Course in Functional Analysis, Graduate Texts in Mathematics, 96 (Springer, New York, 1997).Google Scholar
Cowen, C. and MacCluer, B., Composition Operators on Spaces of Analytic Functions (CRC Press, Boca Raton, FL, 1995).Google Scholar
Hedenmalm, H., Kirenblum, B. and Zhu, K. H., Theory of Bergman Spaces, Graduate Texts in Mathematics, 199 (Springer, New York, 2000).CrossRefGoogle Scholar
Manhas, J. S. and Zhao, R., ‘Fredholm and frame-preserving weighted composition operators’, Complex Anal. Oper. Theory 18 (2024), 34.CrossRefGoogle Scholar
Ortega, J. M. and Fábrega, J., ‘Multipliers in Hardy–Sobolev spaces’, Integral Equations Operator Theory 55 (2006), 535–560.CrossRefGoogle Scholar
Rudin, W., Function Theory in the Unit Ball of
 ${\mathbb{C}}^n$
(Springer, New York, 1980).Google Scholar
${\mathbb{C}}^n$
(Springer, New York, 1980).Google Scholar
Shields, A. L., ‘Weighted shift operators and analytic function theory’, Math. Surveys 13 (1974), 48–128.Google Scholar
Zhu, K. H., Operator Theory in Function Spaces (American Mathematical Society, Providence, RI, 2007).Google Scholar


