No CrossRef data available.
Article contents
CONVOLUTION OPERATORS AND HOMOMORPHISMS OF LOCALLY COMPACT GROUPS
Published online by Cambridge University Press: 01 June 2008
Abstract
Let 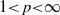 , let G and H belocally compact groups and let ω be a continuous homomorphism of G into H. We prove, if G is amenable, the existence of a linear contraction of the Banach algebra CVp(G) of the p-convolution operators on G into CVp(H) which extends the usual definition of the image of a bounded measure by ω. We also discuss the uniqueness of this linear contraction onto important subalgebras of CVp(G). Even if G and H are abelian, we obtain new results. Let Gd denote the group G provided with a discrete topology. As a corollary, we obtain, for every discrete measure,
, let G and H belocally compact groups and let ω be a continuous homomorphism of G into H. We prove, if G is amenable, the existence of a linear contraction of the Banach algebra CVp(G) of the p-convolution operators on G into CVp(H) which extends the usual definition of the image of a bounded measure by ω. We also discuss the uniqueness of this linear contraction onto important subalgebras of CVp(G). Even if G and H are abelian, we obtain new results. Let Gd denote the group G provided with a discrete topology. As a corollary, we obtain, for every discrete measure, 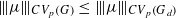 , for Gd amenable. For arbitrary G, we also obtain
, for Gd amenable. For arbitrary G, we also obtain 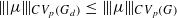 . These inequalities were already known for p=2 . The proofs presented in this paper avoid the use of the Hilbertian techniques which are not applicable to
. These inequalities were already known for p=2 . The proofs presented in this paper avoid the use of the Hilbertian techniques which are not applicable to 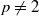 . Finally, for Gd amenable, we construct a natural map of CVp (G)into CVp (Gd) .
. Finally, for Gd amenable, we construct a natural map of CVp (G)into CVp (Gd) .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2008 Australian Mathematical Society

