No CrossRef data available.
Article contents
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
Published online by Cambridge University Press: 02 December 2024
Abstract
For a prime p and a rational elliptic curve 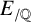 $E_{/\mathbb {Q}}$, set
$E_{/\mathbb {Q}}$, set 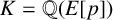 $K=\mathbb {Q}(E[p])$ to denote the torsion field generated by
$K=\mathbb {Q}(E[p])$ to denote the torsion field generated by 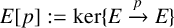 $E[p]:=\operatorname {ker}\{E\xrightarrow {p} E\}$. The class group
$E[p]:=\operatorname {ker}\{E\xrightarrow {p} E\}$. The class group 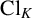 $\operatorname {Cl}_K$ is a module over
$\operatorname {Cl}_K$ is a module over 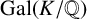 $\operatorname {Gal}(K/\mathbb {Q})$. Given a fixed odd prime number p, we study the average nonvanishing of certain Galois stable quotients of the mod-p class group
$\operatorname {Gal}(K/\mathbb {Q})$. Given a fixed odd prime number p, we study the average nonvanishing of certain Galois stable quotients of the mod-p class group 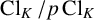 $\operatorname {Cl}_K/p\operatorname {Cl}_K$. Here, E varies over all rational elliptic curves, ordered according to height. Our results are conditional, since we assume that the p-primary part of the Tate–Shafarevich group is finite. Furthermore, we assume predictions made by Delaunay for the statistical variation of the p-primary parts of Tate–Shafarevich groups. We also prove results in the case when the elliptic curve
$\operatorname {Cl}_K/p\operatorname {Cl}_K$. Here, E varies over all rational elliptic curves, ordered according to height. Our results are conditional, since we assume that the p-primary part of the Tate–Shafarevich group is finite. Furthermore, we assume predictions made by Delaunay for the statistical variation of the p-primary parts of Tate–Shafarevich groups. We also prove results in the case when the elliptic curve 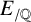 $E_{/\mathbb {Q}}$ is fixed and the prime p is allowed to vary.
$E_{/\mathbb {Q}}$ is fixed and the prime p is allowed to vary.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Michael Coons
From September 2022 to September 2023, the first author’s research is supported by the CRM Simons postdoctoral fellowship.


