Article contents
THE CATENARY AND TAME DEGREES ON A NUMERICAL MONOID ARE EVENTUALLY PERIODIC
Published online by Cambridge University Press: 09 September 2014
Abstract
Let 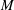 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M$ be a commutative cancellative monoid. For
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M$ be a commutative cancellative monoid. For 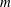 $m$ a nonunit in
$m$ a nonunit in 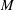 $M$, the catenary degree of
$M$, the catenary degree of 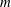 $m$, denoted
$m$, denoted 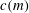 $c(m)$, and the tame degree of
$c(m)$, and the tame degree of 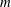 $m$, denoted
$m$, denoted 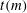 $t(m)$, are combinatorial constants that describe the relationships between differing irreducible factorizations of
$t(m)$, are combinatorial constants that describe the relationships between differing irreducible factorizations of 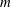 $m$. These constants have been studied carefully in the literature for various kinds of monoids, including Krull monoids and numerical monoids. In this paper, we show for a given numerical monoid
$m$. These constants have been studied carefully in the literature for various kinds of monoids, including Krull monoids and numerical monoids. In this paper, we show for a given numerical monoid 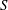 $S$ that the sequences
$S$ that the sequences 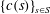 $\{c(s)\}_{s\in S}$ and
$\{c(s)\}_{s\in S}$ and 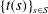 $\{t(s)\}_{s\in S}$ are both eventually periodic. We show similar behavior for several functions related to the catenary degree which have recently appeared in the literature. These results nicely complement the known result that the sequence
$\{t(s)\}_{s\in S}$ are both eventually periodic. We show similar behavior for several functions related to the catenary degree which have recently appeared in the literature. These results nicely complement the known result that the sequence 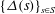 $\{\Delta (s)\}_{s\in S}$ of delta sets of
$\{\Delta (s)\}_{s\in S}$ of delta sets of 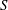 $S$ also satisfies a similar periodicity condition.
$S$ also satisfies a similar periodicity condition.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 289 - 300
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 15
- Cited by

