Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiao, Yong
2011.
Embeddings between weak Orlicz martingale spaces.
Journal of Mathematical Analysis and Applications,
Vol. 378,
Issue. 1,
p.
220.
Jiao, Yong
Wu, Lian
and
Popa, Mihai
2013.
Operator-valued martingale transforms in rearrangement invariant spaces and applications.
Science China Mathematics,
Vol. 56,
Issue. 4,
p.
831.
Yu, Lin
2014.
Duals of Hardy spaces of B-valued martingales for 0 < r ≤ 1.
Acta Mathematica Sinica, English Series,
Vol. 30,
Issue. 8,
p.
1365.
Yu, Lin
2016.
Duality theorem for B‐valued martingale Orlicz–Hardy spaces associated with concave functions.
Mathematische Nachrichten,
Vol. 289,
Issue. 5-6,
p.
756.

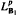 into
into 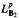 for some
for some 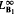 into
into 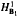 into
into 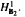 . Applications to
. Applications to 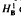 defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.
defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.