Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Navara, Mirko
2008.
Small Quantum Structures with Small State Spaces.
International Journal of Theoretical Physics,
Vol. 47,
Issue. 1,
p.
36.
Jenča, Gejza
2010.
0-homogeneous effect algebras.
Soft Computing,
Vol. 14,
Issue. 10,
p.
1111.
Foulis, David J.
and
Pulmannová, Sylvia
2012.
Quotients of dimension effect algebras.
Algebra universalis,
Vol. 67,
Issue. 1,
p.
81.
Foulis, D. J.
and
Pulmannová, S.
2012.
Logical Connectives on Lattice Effect Algebras.
Studia Logica,
Vol. 100,
Issue. 6,
p.
1291.
Chovanec, Ferdinand
and
Jurečková, Mária
2013.
Fractal properties of MV-algebra pastings.
Fuzzy Sets and Systems,
Vol. 232,
Issue. ,
p.
46.
Yu, Bin
Li, Qingguo
and
Wu, Huanrong
2017.
A new view of relationship between atomic posets and complete (algebraic) lattices.
Open Mathematics,
Vol. 15,
Issue. 1,
p.
238.
Navara, Mirko
and
Voráček, Václav
2021.
Quantum Structures Without Group-Valued Measures.
International Journal of Theoretical Physics,
Vol. 60,
Issue. 2,
p.
687.
Rafiee Rad, Soroush
Sharafi, Amir Hossein
and
Smets, Sonja
2021.
A Complete Axiomatisation for the Logic of Lattice Effect Algebras.
International Journal of Theoretical Physics,
Vol. 60,
Issue. 2,
p.
696.

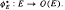 :
: 