Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lee, Tsiu-Kwen
2015.
Additive maps having a generalized derivation expansion.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 04,
p.
1550048.
De Filippis, Vincenzo
2016.
Annihilators and Power Values of Generalized Skew Derivations on Lie Ideals.
Canadian Mathematical Bulletin,
Vol. 59,
Issue. 2,
p.
258.
Liu, Cheng-Kai
2017.
An Engel condition withb-generalized derivations.
Linear and Multilinear Algebra,
Vol. 65,
Issue. 2,
p.
300.
Dhara, Basudeb
and
De Filippis, Vincenzo
2018.
b-Generalized Derivations Acting on Multilinear Polynomials in Prime Rings.
Algebra Colloquium,
Vol. 25,
Issue. 04,
p.
681.
Liau, Pao-Kuei
and
Liu, Cheng-Kai
2018.
An Engel condition with b-generalized derivations for Lie ideals.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 03,
p.
1850046.
Filippis, Vincenzo De
and
Wei, Feng
2018.
$b$-generalized $(\alpha,\beta)$-derivations and $b$-generalized $(\alpha,\beta)$-biderivations of Prime Rings.
Taiwanese Journal of Mathematics,
Vol. 22,
Issue. 2,
De Filippis, Vincenzo
and
Wei, Feng
2018.
b-Generalized Skew Derivations on Lie Ideals.
Mediterranean Journal of Mathematics,
Vol. 15,
Issue. 2,
De Filippis, Vincenzo
and
Wei, Feng
2018.
Centralizers of X-Generalized Skew Derivations on Multilinear Polynomials in Prime Rings.
Communications in Mathematics and Statistics,
Vol. 6,
Issue. 1,
p.
49.
Filippis, Vincenzo De
Scudo, Giovanni
and
Wei, Feng
2021.
Polynomial Identities in Algebras.
Vol. 44,
Issue. ,
p.
109.
Abbasi, Adnan
Mozumder, Muzibur Rahman
and
Jabeen, Aisha
2022.
Algebra and Related Topics with Applications.
Vol. 392,
Issue. ,
p.
3.
Raza, Mohd Arif
Khan, Abdul Nadim
and
Alhazmi, Husain
2022.
A characterization of $ b- $generalized derivations on prime rings with involution.
AIMS Mathematics,
Vol. 7,
Issue. 2,
p.
2413.
Pehlivan, T.
and
Albaş, E.
2022.
b
-Generalized derivations on prime rings.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 74,
Issue. 6,
p.
832.
Khan, Mohammad Salahuddin
2022.
Algebra and Related Topics with Applications.
Vol. 392,
Issue. ,
p.
181.
Dhara, B.
Kar, S.
and
Bera, M.
2022.
X-generalized skew derivations with annihilating and centralizing conditions in prime rings.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 68,
Issue. 1,
p.
147.
Carini, Luisa
and
De Filippis, Vincenzo
2022.
Algebra and Related Topics with Applications.
Vol. 392,
Issue. ,
p.
59.
Pehlivan, T.
and
Albaş, E.
2022.
b-Generalized Derivations on Prime Rings.
Ukrainian Mathematical Journal,
Vol. 74,
Issue. 6,
p.
953.
Bera, Nripendu
Dhara, Basudeb
and
Kar, Sukhendu
2023.
A result concerning b-generalized skew derivations on multilinear polynomials in prime rings.
Communications in Algebra,
Vol. 51,
Issue. 3,
p.
887.
Gupta, Charu
2023.
On b-generalized derivations in prime rings.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 72,
Issue. 4,
p.
2703.
Carini, Luisa
and
Scudo, Giovanni
2023.
On Posner’s theorem with b-generalized skew derivations on Lie ideals.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 03,
De Filippis, Vincenzo
Scudo, Giovanni
and
Wei, Feng
2024.
On X-generalized skew derivations and their applications.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 03,
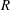 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}R$ be a semiprime ring with extended centroid
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}R$ be a semiprime ring with extended centroid 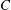 $C$ and with maximal right ring of quotients
$C$ and with maximal right ring of quotients 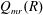 $Q_{mr}(R)$. Let
$Q_{mr}(R)$. Let 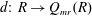 $d{:}\ R\to Q_{mr}(R)$ be an additive map and
$d{:}\ R\to Q_{mr}(R)$ be an additive map and 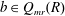 $b\in Q_{mr}(R)$. An additive map
$b\in Q_{mr}(R)$. An additive map 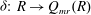 $\delta {:}\ R\to Q_{mr}(R)$ is called a (left)
$\delta {:}\ R\to Q_{mr}(R)$ is called a (left) 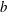 $b$-generalized derivation with associated map
$b$-generalized derivation with associated map 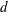 $d$ if
$d$ if 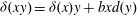 $\delta (xy)=\delta (x)y+bxd(y)$ for all
$\delta (xy)=\delta (x)y+bxd(y)$ for all 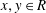 $x, y\in R$. This gives a unified viewpoint of derivations, generalized derivations and generalized
$x, y\in R$. This gives a unified viewpoint of derivations, generalized derivations and generalized  $\sigma $-derivations with an X-inner automorphism
$\sigma $-derivations with an X-inner automorphism  $\sigma $. We give a complete characterization of
$\sigma $. We give a complete characterization of 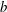 $b$-generalized derivations of
$b$-generalized derivations of 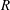 $R$ having nilpotent values of bounded index. This extends several known results in the literature.
$R$ having nilpotent values of bounded index. This extends several known results in the literature.
