Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Giulini, Saverio
1986.
Approximation and Besov spaces on stratified groups.
Proceedings of the American Mathematical Society,
Vol. 96,
Issue. 4,
p.
569.
Colzani, Leonardo
and
Masiero, Federica
2003.
Approximation of eigenfunctions of elliptic differential operators.
Journal of Approximation Theory,
Vol. 123,
Issue. 1,
p.
13.
Dmytryshyn, Marian
and
Lopushansky, Oleh
2014.
Bernstein-Jackson-type inequalities and Besov spaces associated with unbounded operators.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Dmytryshyn, Marian
and
Lopushansky, Oleh
2019.
On Spectral Approximations of Unbounded Operators.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 8,
p.
3659.
Dmytryshyn, M.I.
2021.
Approximation by interpolation spectral subspaces of operators with discrete spectrum.
Matematychni Studii,
Vol. 55,
Issue. 2,
p.
162.
Bruno, Tommaso
Peloso, Marco M.
and
Vallarino, Maria
2023.
Pointwise multipliers for Triebel–Lizorkin and Besov spaces on Lie groups.
Bulletin des Sciences Mathématiques,
Vol. 188,
Issue. ,
p.
103320.
El Ouadih, S.
2024.
Direct and inverse approximation theorems for functions defined in Damek–Ricci spaces.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 76,
Issue. 8,
p.
1132.
Ouadih, S. El
2025.
Direct and Inverse Approximation Theorems for Functions Defined in Damek–Ricci Spaces.
Ukrainian Mathematical Journal,
Vol. 76,
Issue. 8,
p.
1284.

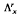 by the behavior of their best approximations by functions in the space
by the behavior of their best approximations by functions in the space 