No CrossRef data available.
Article contents
Approximation by a sum of polynomials of different degrees involving primes
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let λj (1 ≦ j ≦ 4) be any nonzero real numbers which are not all of the same sign and not all in rational ratio and let pj be polynomials of degree one or two with integer coefficients and positive leading coefficients. The author proves that if exactly two pj are of degree two then for any real n there are infinitely many solutions in primes pj of the inequality 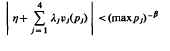 . where 0 <β < (√(21)–1)∖5760.
. where 0 <β < (√(21)–1)∖5760.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1979
References
Baker, A. (1967), ‘On some diophantine inequalities involving primes’, J. Reine Angew. Math. 228, 166–181.Google Scholar
Davenport, H. and Heilbronn, H. (1946), ‘On indefinite quadratic forms in five variables’, J. London Math. Soc. 21, 185–193.CrossRefGoogle Scholar
Davenport, H. and Roth, K. F. (1955), ‘The solubility of certain diophantine inequalities’, Mathematika 2, 81–96.CrossRefGoogle Scholar
Hardy, G. and Wright, E. M. (1960), An introduction to the theory of numbers (4th ed., Clarendon Press, Oxford).Google Scholar
Hua, L. K. (1965), Additive theory of prime numbers, Translations of Mathematical Monographs, Vol. 13 (Amer. Math. Soc., Providence, R.I.).Google Scholar
Ingham, A. E., ‘On the estimation of N(σ, T)’, Quart. J. Math. Oxford. 11 (1940), 291–292.Google Scholar
Liu, M. C. (1977), ‘Diophantine approximation involving primes’, J. Reine Angew. Math. 289, 199–208.Google Scholar
Liu, M. C. (1978), ‘Approximation by a sum of polynomials involving primes’, J. Math. Soc. Japan, 30, 395–412.CrossRefGoogle Scholar
Schwarz, W. (1963), ‘Über die Lösbarkeit gewisser Ungleichungen durch Primzahlen’, J. Reine Angew. Math. 212, 150–157.CrossRefGoogle Scholar
Vaughan, R. C. (1974a), ‘Diophantine approximation by prime numbers, I’, Proc. London Math. Soc. (3) 28, 373–384.CrossRefGoogle Scholar
Vaughan, R. C. (1974b), ‘Diophantine approximation by prime numbers, II’, Proc. London Math. Soc. (3), 28, 385–401.CrossRefGoogle Scholar
Vinogradov, I. M. (1938), ‘A new estimation of a trigonometric sum containing primes’ (in Russian with English summary), Bull. Acad. Sci. USSR, Sér. Math. 2, 3–13.Google Scholar

