Hostname: page-component-7dd5485656-c8zdz Total loading time: 0 Render date: 2025-10-30T22:14:27.521Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SMOOTHNESS OF ORBITAL MEASURES ON NONCOMPACT SYMMETRIC SPACES

Part of: Lie groups Abstract harmonic analysis

Published online by Cambridge University Press:  26 April 2021

SANJIV KUMAR GUPTA  and
KATHRYN E. HARE
SANJIV KUMAR GUPTA
Affiliation:
Dept. of Mathematics, Sultan Qaboos University, P.O. Box 36, Muscat, Al Khodh 123, Sultanate of Oman e-mail: gupta@squ.edu.om
KATHRYN E. HARE*
Affiliation:
Dept. of Pure Mathematics, University of Waterloo, Waterloo, ON N2L 3G1, Canada
*
e-mail: kehare@uwaterloo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 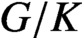$G/K$ be an irreducible symmetric space, where G is a noncompact, connected Lie group and K is a compact, connected subgroup. We use decay properties of the spherical functions to show that the convolution product of any 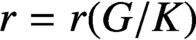$r=r(G/K)$ continuous orbital measures has its density function in 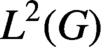$L^{2}(G)$ and hence is an absolutely continuous measure with respect to the Haar measure. The number r is approximately the rank of 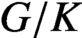$G/K$. For the special case of the orbital measures, 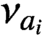$\nu _{a_{i}}$, supported on the double cosets 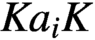$Ka_{i}K$, where 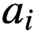$a_{i}$ belongs to the dense set of regular elements, we prove the sharp result that 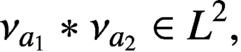$\nu _{a_{1}}\ast \nu _{a_{2}}\in L^{2},$ except for the symmetric space of Cartan class 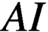$AI$ when the convolution of three orbital measures is needed (even though $\nu _{a_{1}}\ast \nu _{a_{2}}$ is absolutely continuous).

Keywords

orbital measurespherical functionsymmetric space

MSC classification

Primary: 43A90: Spherical functions
Secondary: 43A85: Analysis on homogeneous spaces 22E30: Analysis on real and complex Lie groups

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 2 , October 2022 , pp. 188 - 207
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Robert Yuncken

This research is supported in part by NSERC 2016-03719 and by Sultan Qaboos University. The authors thank Acadia University for their hospitality when this research was done.

References

Abramowitz, M. and Stegun, I., Handbook of Mathematical Functions , National Bureau of Standards Applied Mathematics Series, 55 (U.S. Government Printing Office, Washington, DC, 1970).Google Scholar
Anchouche, B., ‘Regularity of the Radon–Nikodym derivative of a convolution of orbital measures on noncompact symmetric spaces’, Preprint, 2018.CrossRefGoogle Scholar
Anchouche, B., Gupta, S. K. and Plagne, A., ‘Orbital measures on $\mathrm{SU}(2)/\mathrm{SO}(2)$ ’, Monatsh. Math. 178 (2015), 493–520.CrossRefGoogle Scholar
Anker, J. P., ‘The spherical Fourier transform of rapidly decreasing functions. A simple proof of a characterization due to Harish-Chandra, Helgason, Trombi and Varadarajan’, J. Funct. Anal. 96 (1991), 331–349.CrossRefGoogle Scholar
Caselle, M. and Magnea, U., ‘Random matrix theory and symmetric spaces’, Phys. Rep. 394 (2004), 41–156.CrossRefGoogle Scholar
Duistermaat, J. J., Kolk, J. A. C. and Varadarajan, V. S., ‘Functions, flows and oscillatory integrals on flag manifolds and conjugacy classes in semisimple Lie groups’, Compos. Math. 49 (1983), 309–398.Google Scholar
Fitouhi, A. and Hamza, M., ‘A uniform expansion for the eigenfunction of a singular second-order differential operator’, SIAM J. Math. Anal. 21 (1990), 1619–1632.CrossRefGoogle Scholar
Graczyk, P. and Sawyer, P., ‘Absolute continuity of convolutions of orbital measures on Riemannian symmetric spaces’, J. Funct. Anal. 259 (2010), 1759–1770.CrossRefGoogle Scholar
Graczyk, P. and Sawyer, P., ‘A sharp criterion for the existence of the product formula on symmetric spaces of type ${A}_n$ ’, J. Lie Theory 20 (2010), 751–766.Google Scholar
Graczyk, P. and Sawyer, P., ‘Convolution of orbital measures on symmetric spaces of type ${C}_p$ and ${D}_p$ ’, J. Aust. Math. Soc. 98 (2015), 232–256.CrossRefGoogle Scholar
Graczyk, P. and Sawyer, P., ‘Convolution of orbital measures on symmetric spaces: a survey’, Contemp. Math. 668 (2016), 81–110.CrossRefGoogle Scholar
Gupta, S. K. and Hare, K. E., ‘ ${L}^2$ -singular dichotomy for orbital measures of classical compact Lie groups’, Adv. Math. 222 (2009), 1521–1573.CrossRefGoogle Scholar
Gupta, S. K. and Hare, K. E., ‘The absolute continuity of convolutions of orbital measures in symmetric spaces’, J. Math. Anal. Appl. 450 (2017), 81–111.CrossRefGoogle Scholar
Gupta, S. K., Hare, K. E. and Seyfaddini, S., ‘ ${L}^2$ -singular dichotomy for orbital measures of classical simple Lie algebras’, Math. Z. 262 (2009), 91–124.CrossRefGoogle Scholar
Hare, K. E. and Skoufranis, P., ‘The smoothness of orbital measures on exceptional Lie groups and algebras’, J. Lie Theory 21 (2011), 987–1007.Google Scholar
Hare, K. E., Wilson, D. and Yee, W. L., ‘Pointwise estimates of the size of characters of compact Lie groups’, J. Aust. Math. Soc. 69 (2000), 61–84.CrossRefGoogle Scholar
Hare, K. E. and Yeats, K., ‘The size of characters of exceptional Lie groups’, J. Aust. Math. Soc. 77 (2004), 233–248.CrossRefGoogle Scholar
Helgason, S., Differential Geometry, Lie Groups and Symmetric Spaces (Academic Press, New York, 1978).Google Scholar
Helgason, S., Groups and Geometric Analysis (Academic Press, Orlando, FL, 1984).Google Scholar
Humphreys, J., Introduction to Lie Algebras and Representation Theory (Springer, New York, 1994).Google Scholar
Ragozin, D., ‘Zonal measure algebras on isotropy irreducible homogeneous spaces’, J. Funct. Anal. 17 (1974), 355–376.CrossRefGoogle Scholar
Wolf, J., ‘ Harmonic Analysis on Commutative Spaces ’, AMS Mathematical Surveys and Monographs, 142 (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar