No CrossRef data available.
Article contents
ON THE ALGEBRAS 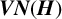 $\boldsymbol {VN(H)}$ AND
$\boldsymbol {VN(H)}$ AND 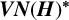 $\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP
$\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP 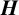 $\boldsymbol {H}$
$\boldsymbol {H}$
Published online by Cambridge University Press: 12 December 2022
Abstract
Let H be an ultraspherical hypergroup and let 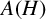 $A(H)$ be the Fourier algebra associated with
$A(H)$ be the Fourier algebra associated with 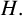 $H.$ In this paper, we study the dual and the double dual of
$H.$ In this paper, we study the dual and the double dual of 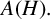 $A(H).$ We prove among other things that the subspace of all uniformly continuous functionals on
$A(H).$ We prove among other things that the subspace of all uniformly continuous functionals on 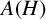 $A(H)$ forms a
$A(H)$ forms a 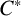 $C^*$-algebra. We also prove that the double dual
$C^*$-algebra. We also prove that the double dual 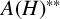 $A(H)^{\ast \ast }$ is neither commutative nor semisimple with respect to the Arens product, unless the underlying hypergroup H is finite. Finally, we study the unit elements of
$A(H)^{\ast \ast }$ is neither commutative nor semisimple with respect to the Arens product, unless the underlying hypergroup H is finite. Finally, we study the unit elements of 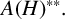 $A(H)^{\ast \ast }.$
$A(H)^{\ast \ast }.$
Keywords
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 115 , Issue 3 , December 2023 , pp. 337 - 353
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by George Willis



