Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mishina, A. P.
1995.
Abelian groups.
Journal of Mathematical Sciences,
Vol. 76,
Issue. 6,
p.
2721.
Göbel, Rüdiger
2000.
Infinite Length Modules.
p.
107.
Göbel, Rüdiger
and
Shelah, Saharon
2000.
Cotorsion theories and splitters.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 11,
p.
5357.
Schultz, P.
2001.
Self-splitting Abelian groups.
Bulletin of the Australian Mathematical Society,
Vol. 64,
Issue. 1,
p.
71.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
143.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
527.
Eklof, Paul C.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
85.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
17.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
476.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
441.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
1.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
191.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
55.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
563.
Eklof, Paul C.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
363.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
316.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
498.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
123.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
292.
Eklof, Paul C.
and
Mekler, Alan H.
2002.
Almost Free Modules - Set-theoretic Methods.
Vol. 65,
Issue. ,
p.
401.

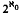 is cotorsion, is
is cotorsion, is 