Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-30T06:32:02.984Z Has data issue: false hasContentIssue false
  • English
  • Français

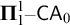THE WEIHRAUCH LATTICE AT THE LEVEL OF $\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM

Part of: Set theory Computability and recursion theory General logic

Published online by Cambridge University Press:  27 January 2025

VITTORIO CIPRIANI Open the ORCID record for VITTORIO CIPRIANI [Opens in a new window] ,
ALBERTO MARCONE Open the ORCID record for ALBERTO MARCONE [Opens in a new window]  and
MANLIO VALENTI Open the ORCID record for MANLIO VALENTI [Opens in a new window]
VITTORIO CIPRIANI*
Affiliation:
DIPARTIMENTO DI SCIENZE MATEMATICHE INFORMATICHE E FISICHE UNIVERSITÀ DI UDINE ITALY Current address: INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY TECHNISCHE UNIVERSITÄT WIEN AUSTRIA E-mail: vittorio.cipriani17@gmail.com
ALBERTO MARCONE
Affiliation:
DIPARTIMENTO DI SCIENZE MATEMATICHE INFORMATICHE E FISICHE UNIVERSITÀ DI UDINE ITALY E-mail: alberto.marcone@uniud.it
MANLIO VALENTI
Affiliation:
DIPARTIMENTO DI SCIENZE MATEMATICHE INFORMATICHE E FISICHE UNIVERSITÀ DI UDINE ITALY and DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN - MADISON MADISON USA Current address: DEPARTMENT OF COMPUTER SCIENCE SWANSEA UNIVERSITY UK E-mail: manliovalenti@gmail.com
*
E-mail: vittorio.cipriani17@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper continues the program connecting reverse mathematics and computable analysis via the framework of Weihrauch reducibility. In particular, we consider problems related to perfect subsets of Polish spaces, studying the perfect set theorem, the Cantor–Bendixson theorem, and various problems arising from them. 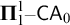In the framework of reverse mathematics, these theorems are equivalent, respectively, to $\mathsf {ATR}_0$ and $\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$, the two strongest subsystems of second order arithmetic among the so-called big five. As far as we know, this is the first systematic study of problems at the level of 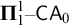$\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$ in the Weihrauch lattice. We show that the strength of some of the problems we study depends on the topological properties of the Polish space under consideration, while others have the same strength once the space is rich enough.

Keywords

computable analysisWeihrauch degreesdescriptive set theoryperfect setsCantor-Bendixson theoremreverse mathematics

MSC classification

Primary: 03D78: Computation over the reals
Secondary: 03E15: Descriptive set theory 03B30: Foundations of classical theories (including reverse mathematics) 03D30: Other degrees and reducibilities
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 39
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anglès d’Auriac, P.-E. and Kihara, T., A comparison of various analytic choice principles . Journal of Symbolic Logic , vol. 86 (2021), no. 4, pp. 1452–1485.CrossRefGoogle Scholar
Brattka, V., Effective Borel measurability and reducibility of functions . Mathematical Logic Quarterly , vol. 51 (2005), no. 1, pp. 19–44.CrossRefGoogle Scholar
Brattka, V., de Brecht, M., and Pauly, A., Closed choice and a uniform low basis theorem . Annals of Pure and Applied Logic , vol. 163 (2012), no. 8, pp. 986–1008.CrossRefGoogle Scholar
Brattka, V. and Gherardi, G., Borel complexity of topological operations on computable metric spaces . Journal of Logic and Computation , vol. 19 (2009), no. 1, pp. 45–76.CrossRefGoogle Scholar
Brattka, V. and Gherardi, G., Weihrauch degrees, omniscience principles and weak computability . Journal of Symbolic Logic , vol. 76 (2011), no. 1, pp. 143–176.CrossRefGoogle Scholar
Brattka, V. and Gherardi, G., Completion of choice . Annals of Pure and Applied Logic , vol. 172 (2021), no. 3, Paper No. 102914, 30 pp.CrossRefGoogle Scholar
Brattka, V., Gherardi, G., and Marcone, A., The Bolzano–Weierstrass theorem is the jump of weak König’s lemma . Annals of Pure and Applied Logic , vol. 163 (2012), no. 6, pp. 623–655.CrossRefGoogle Scholar
Brattka, V., Gherardi, G., and Pauly, A., Weihrauch complexity in computable analysis , Handbook of Computability and Complexity in Analysis (Brattka, V. and Hertling, P., editors), Springer International Publishing, Cham 2021, pp. 367–417.CrossRefGoogle Scholar
Brattka, V., Kawamura, A., Marcone, A., and Pauly, A., Measuring the complexity of computational content (Dagstuhl seminar 15392) . Dagstuhl Reports , vol. 5 (2016), no. 9, pp. 77–104.Google Scholar
Brattka, V. and Pauly, A., On the algebraic structure of Weihrauch degrees . Logical Methods in Computer Science , vol. 14 (2018), no. 4, pp. 1–36.Google Scholar
Dzhafarov, D. D., Solomon, R., and Yokoyama, K., On the first-order parts of problems in the Weihrauch degrees . Computability , vol. 13 (2024), no. 3-4, pp. 363–375.Google Scholar
Gherardi, G. and Marcone, A., How incomputable is the separable Hahn-Banach theorem? Notre Dame Journal of Formal Logic , vol. 50 (2009), no. 4, pp. 393–425.CrossRefGoogle Scholar
Hirst, J. L., Leaf management . Computability , vol. 9 (2020), no. 3–4, pp. 309–314.CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory , first ed., Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
Kihara, T., Marcone, A., and Pauly, A., Searching for an analogue of ATR_0 in the Weihrauch lattice . Journal of Symbolic Logic , vol. 85(2020), no. 3, pp. 1006–1043.CrossRefGoogle Scholar
Le Goh, J., Some computability-theoretic reductions between principles around $AT{R}_0$ , Preprint, 2019, arXiv:1905.06868.Google Scholar
Le Goh, J., Embeddings between well-orderings: Computability-theoretic reductions . Annals of Pure and Applied Logic , vol. 171 (2020), no. 6, Paper No. 102789, 17 pp.Google Scholar
Le Goh, J., Pauly, A., and Valenti, M., Finding descending sequences through ill-founded linear orders . Journal of Symbolic Logic , vol. 86 (2021), no. 2, pp. 817–854.CrossRefGoogle Scholar
Marcone, A. and Valenti, M., The open and clopen Ramsey theorems in the Weihrauch lattice . Journal of Symbolic Logic , vol. 86 (2021), no. 1, pp. 316–351.CrossRefGoogle Scholar
Moschovakis, Y. N., Descriptive Set Theory , second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.CrossRefGoogle Scholar
Nobrega, H. and Pauly, A., Game characterizations and lower cones in the Weihrauch degrees . Logical Methods in Computer Science , vol. 15 (2019), no. 3, pp. 11:1–11:29.Google Scholar
Pauly, A., On the topological aspects of the theory of represented spaces . Computability , vol. 5 (2016), no. 2, pp. 159–180.CrossRefGoogle Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability , first ed., McGraw-Hill Book Co., New York–Toronto–London, 1967.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , second ed., Perspectives in Logic, Cambridge University Press and Association for Symbolic Logic, Cambridge and Poughkeepsie, NY, 2009.CrossRefGoogle Scholar
Soldà, G. and Valenti, M., Algebraic properties of the first-order part of a problem . Annals of Pure and Applied Logic , vol. 174 (2023), no. 7, Paper No. 103270, 41 pp.CrossRefGoogle Scholar
Weihrauch, K., Computable Analysis: An Introduction , first ed., Texts in Theoretical Computer Science. An EATCS Series, Springer-Verlag, Berlin, 2000.CrossRefGoogle Scholar