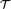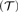Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moore, Matthew
2016.
The variety generated by $${\mathbb {A}(\mathcal {T})}$$ A ( T ) – two counterexamples.
Algebra universalis,
Vol. 75,
Issue. 1,
p.
21.
Moore, Matthew
2019.
Finite degree clones are undecidable.
Theoretical Computer Science,
Vol. 796,
Issue. ,
p.
237.