Article contents
Uncountable master codes and the jump hierarchy
Published online by Cambridge University Press: 12 March 2014
Extract
The Turing jump can easily be iterated any finite number of times. The challenge is posed by by transfinite iterations. a(ω) has an intuitively compelling definition: {‹m, n›: n ∈ a(m)}. Starting with Putnam et al. [1], [2], [9] and culminating in Jockusch-Simpson [8] and Hodes [6], recent work has justified this ω-jump and extended it through 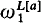 .
.
Of great use are the master codes of Jensen [3], [7]. Briefly, a Δn(Lβ)-master code is a complete Δn(Lβ) set of ordinals, with supremum as small as possible. Connections with classical recursion theory are tight. When the Δn(Lβ) master codes are reals, they are Turing equivalent. If a is a Δn(Lβ) MC, then a′ is a Δn + 1(Lβ) MC. Intuitively satisfying transfinite jumps, such as the ω-jump above, produce a Turing jump hierarchy equal to an initial segment of the master codes.
Hodes capitalized on these facts by defining 0α, α < 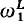 , set-theoretically as the degree of the αth MC which is a real, and then proving the equivalence of a jump-theoretic definition of 0α. The successor codes are jumps of their predecessors, and for a limit λ, 0λ is the minimum of a set of degrees associated with {0α: α: < λ}.
, set-theoretically as the degree of the αth MC which is a real, and then proving the equivalence of a jump-theoretic definition of 0α. The successor codes are jumps of their predecessors, and for a limit λ, 0λ is the minimum of a set of degrees associated with {0α: α: < λ}.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
REFERENCES
- 1
- Cited by

