Article contents
Über eine Art von Unvollständigkeit des Prädikatenkalküls der ersten Stufe
Published online by Cambridge University Press: 12 March 2014
Extract
Nach Gödel ist der Prädikatenkalkül der ersten Stufe vollständig in dem Sinne, daβ alle identischen Ausdrücke dieses Kalküls ableitbar sind. Für den einstelligen Prädikatenkalkül gilt darüber hinaus, daβ zwei Ausdrücke 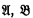 deduktionsgleich (HB I, p. 149) sind, wenn sie für dieselben Individuenbereiche identisch bzw. nicht identisch sind. Solche Ausdrücke mögen identitätsverbunden heiβen. Daβ umgekehrt deduktionsgleiche Ausdrücke identitätsverbunden sind, gilt auch für den vollen Prädikatenkalkül. Dagegen gibt es dort Ausdrücke, die identitätsverbunden, aber nicht deduktionsgleich sind. Solche Ausdrücke sind die in HB I, p. 123, 124 angegebenen
deduktionsgleich (HB I, p. 149) sind, wenn sie für dieselben Individuenbereiche identisch bzw. nicht identisch sind. Solche Ausdrücke mögen identitätsverbunden heiβen. Daβ umgekehrt deduktionsgleiche Ausdrücke identitätsverbunden sind, gilt auch für den vollen Prädikatenkalkül. Dagegen gibt es dort Ausdrücke, die identitätsverbunden, aber nicht deduktionsgleich sind. Solche Ausdrücke sind die in HB I, p. 123, 124 angegebenen 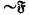 und
und 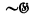 , die beide genau im Endlichen identisch, also identitätsverbunden sind. Die Frage der gegenseitigen Ableitbarkeit bleibt dort allerdings noch unentschieden. Ich werde im Folgenden die gegenseitige Nichtableitbarkeit von
, die beide genau im Endlichen identisch, also identitätsverbunden sind. Die Frage der gegenseitigen Ableitbarkeit bleibt dort allerdings noch unentschieden. Ich werde im Folgenden die gegenseitige Nichtableitbarkeit von 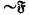 und
und 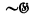 im Prädikatenkalkül der ersten Stufe beweisen. Daraus folgt dann, daβ für den vollen Prädikatenkalkül die Bernayssche Deduktionsgleichheit nicht mit der Identitätsverbundenheit zusammenfällt. Es sei erwähnt, daβ die Identitätsverbundenheit sich zwar in der “Protosyntax” (d.h. metasprachliches “Alle” und “Es gibt” beschränkt auf Zeichenreihen) definieren läβt. Trotzdem kann man nicht von einer verschärften Vollständigkeit des Prädikatenkalküls sprechen; denn es läβt sich zeigen, daβ die Identitätsverbundenheit keine Beziehung vom Typ der Beweisbarkeit ist.
im Prädikatenkalkül der ersten Stufe beweisen. Daraus folgt dann, daβ für den vollen Prädikatenkalkül die Bernayssche Deduktionsgleichheit nicht mit der Identitätsverbundenheit zusammenfällt. Es sei erwähnt, daβ die Identitätsverbundenheit sich zwar in der “Protosyntax” (d.h. metasprachliches “Alle” und “Es gibt” beschränkt auf Zeichenreihen) definieren läβt. Trotzdem kann man nicht von einer verschärften Vollständigkeit des Prädikatenkalküls sprechen; denn es läβt sich zeigen, daβ die Identitätsverbundenheit keine Beziehung vom Typ der Beweisbarkeit ist.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1950
References
1 Im Folgenden Abkürzung für: Hilbert-Bernays, , Grundlagen der Mathematik I (1934)Google Scholar.
2 Dies nimmt man etwa aus der Lösung des Entscheidungs problems (identisch = allgemeingültig).
3 Nach einem Vorschlag von H. Scholz.
4 Dort ![]() .
.
5 Diese Fragestellung geht zurück auf H. Scholz, der die vorliegende Untersuchung angeregt hat. Vgl. Scholz, H., Grundzüge der mathematischen Logik I, §75, 10.7. (1949)Google Scholar.
6 D.h. die korrespondierende Paarmenge von Gödelnummern ist nicht rekursiv aufzählbar. Zur genauen Diskussion hätte man etwa heranzuziehen: Mostowski, A., On definable sets of positive integers, Fundamenta Mathematicae vol. 34 (1946), pp. 81–112CrossRefGoogle Scholar.
7 Mit der Regel der prädikatenlogischen Einsetzung von ![]() für Aab ist gleichwertig die Einsetzung von
für Aab ist gleichwertig die Einsetzung von ![]() für A in Verbindung mit dem Axiomenschema
für A in Verbindung mit dem Axiomenschema ![]() . Die Verwendung des "λ" ist in den folgenden Beweisen zweckmäβig, kann aber grundsätzlich vermieden werden.
. Die Verwendung des "λ" ist in den folgenden Beweisen zweckmäβig, kann aber grundsätzlich vermieden werden.
8 ![]() stehe als Abkürzung für
stehe als Abkürzung für ![]() für
für ![]() Wenn nicht ausdrücklich anders angegeben, sollen bei der Argumentschreibweise für Ausdrücke stets alle vorkommenden freien Variablen aufgeführt sein.
Wenn nicht ausdrücklich anders angegeben, sollen bei der Argumentschreibweise für Ausdrücke stets alle vorkommenden freien Variablen aufgeführt sein.
9 Vgl. Anm. 7.
10 Hier und im Folgenden werden zur inhaltlichen Mitteilung dieselben Zeichen benutzt, die auch in formalen Ausdrücken auftreten. Die Bedeutung im einzelnen Fall ergibt sich aus dem Zusammenhang.
11 Die zweistelligen logischen Funktionen werden hier mit ebenen Punktmengen identifiziert.
12 D.h.: inbezug auf R und ![]() isomorphen Abbildungen von J auf sich.
isomorphen Abbildungen von J auf sich.
13 D.h.: Intervalle der durch ![]() erzeugten Zerlegung von (0, 1).
erzeugten Zerlegung von (0, 1).
14 Dasselbe Resultat hätte man auch wie unter IV (2) durch Ausschaltung der gebundenen Variablen und Diskussion der freien Ausdrücke erhalten können.
- 4
- Cited by

