Published online by Cambridge University Press: 12 March 2014
In [14] J. Hirschfeld established the close connection of models of the true AE sentences of Peano Arithmetic and homomorphic images of the semiring of recursive functions. This fragment of Arithmetic includes most of the familiar results of classical number theory. There are two nice ways that such models appear in the isols. One way was introduced by A. Nerode in [20] and is referred to in the literature as Nerode Semirings. The other way is called a tame model. It is very similar to a Nerode Semiring and was introduced in [6]. The model theoretic properties of Nerode Semirings and tame models have been widely studied by T. G. McLaughlin ([16], [17], and [18]).
In this paper we introduce a new variety of tame model called a torre model. It has as a generator an infinite regressive isol with a nice structural property relative to recursively enumerable sets and their extensions to the isols. What is then obtained is a nonstandard model in the isols of the 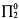 fragment of Peano Arithmetic with the following property: Let T be a torre model. Let f be any recursive function, and let fΛ be its extension to the isols. If there is an isol A with fΛ(A) ϵ T, then there is also an isol B ϵ T with fΛ(B) = fΛ(A).
fragment of Peano Arithmetic with the following property: Let T be a torre model. Let f be any recursive function, and let fΛ be its extension to the isols. If there is an isol A with fΛ(A) ϵ T, then there is also an isol B ϵ T with fΛ(B) = fΛ(A).