Published online by Cambridge University Press: 12 March 2014
The paper is aimed at studying the topological dimension for sets definable in weakly o-minimal structures in order to prepare background for further investigation of groups, group actions and fields definable in the weakly o-minimal context. We prove that the topological dimension of a set definable in a weakly o-minimal structure is invariant under definable injective maps, strengthening an analogous result from [2] for sets and functions definable in models of weakly o-minimal theories. We pay special attention to large subsets of Cartesian products of definable sets, showing that if X, Y and S are non-empty definable sets and S is a large subset of X × Y. then for a large set of tuples 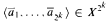 , where k = dim(Y), the union of fibers
, where k = dim(Y), the union of fibers 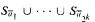 is large in Y. Finally, given a weakly o-minimal structure
is large in Y. Finally, given a weakly o-minimal structure 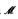 , we find various conditions equivalent to the fact that the topological dimension in
, we find various conditions equivalent to the fact that the topological dimension in 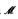 enjoys the addition property.
enjoys the addition property.