Article contents
Taxonomies of model-theoretically defined topological properties
Published online by Cambridge University Press: 12 March 2014
Abstract
A topological classification scheme consists of two ingredients: (1) an abstract class 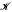 of topological spaces; and (2) a “taxonomy”, i.e. a list of first order sentences, together with a way of assigning an abstract class of spaces to each sentence of the list so that logically equivalent sentences are assigned the same class.
of topological spaces; and (2) a “taxonomy”, i.e. a list of first order sentences, together with a way of assigning an abstract class of spaces to each sentence of the list so that logically equivalent sentences are assigned the same class. 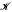 is then endowed with an equivalence relation, two spaces belonging to the same equivalence class if and only if they lie in the same classes prescribed by the taxonomy. A space X in
is then endowed with an equivalence relation, two spaces belonging to the same equivalence class if and only if they lie in the same classes prescribed by the taxonomy. A space X in 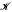 is characterized within the classification scheme if whenever Y ∊
is characterized within the classification scheme if whenever Y ∊ 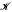 and Y is equivalent to X, then Y is homeomorphic to X. As prime example, the closed set taxonomy assigns to each sentence in the first order language of bounded lattices the class of topological spaces whose lattices of closed sets satisfy that sentence. It turns out that every compact two-complex is characterized via this taxonomy in the class of metrizable spaces, but that no infinite discrete space is so characterized. We investigate various natural classification schemes, compare them, and look into the question of which spaces can and cannot be characterized within them.
and Y is equivalent to X, then Y is homeomorphic to X. As prime example, the closed set taxonomy assigns to each sentence in the first order language of bounded lattices the class of topological spaces whose lattices of closed sets satisfy that sentence. It turns out that every compact two-complex is characterized via this taxonomy in the class of metrizable spaces, but that no infinite discrete space is so characterized. We investigate various natural classification schemes, compare them, and look into the question of which spaces can and cannot be characterized within them.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 7
- Cited by

