Article contents
A structure theorem for semibounded sets in the reals
Published online by Cambridge University Press: 12 March 2014
Extract
In [MPP] it was shown that in every reduct 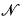 of
of 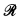 = ‹ ℝ, +, ·, <› that properly expands ℳ = ‹ℝ, +, <, λa›a∈ℝ, all the bounded semi-algebraic (that is,
= ‹ ℝ, +, ·, <› that properly expands ℳ = ‹ℝ, +, <, λa›a∈ℝ, all the bounded semi-algebraic (that is, 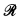 -definable) sets are definable. Said differently, every such
-definable) sets are definable. Said differently, every such 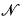 is an expansion of
is an expansion of 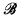 = ‹ℝ, +, <, λa, Bi›a∈ℝ, i∈I where {Bi}i∈I is the collection of all bounded semialgebraic sets and the λa's are scalar multiplication by a. In [PSS] (see Theorem 1.2 below) it was shown that the structure
= ‹ℝ, +, <, λa, Bi›a∈ℝ, i∈I where {Bi}i∈I is the collection of all bounded semialgebraic sets and the λa's are scalar multiplication by a. In [PSS] (see Theorem 1.2 below) it was shown that the structure 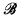 is a proper reduct of
is a proper reduct of 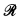 ; that is, one cannot define in it all the semialgebraic sets. In [Pe] we show that
; that is, one cannot define in it all the semialgebraic sets. In [Pe] we show that 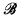 is the only reduct properly between ℳ and
is the only reduct properly between ℳ and 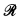 . As a first step towards this result, we investigate in this paper the definable sets in reducts such as
. As a first step towards this result, we investigate in this paper the definable sets in reducts such as 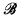 . (We point out that ‘definable’ will always mean ‘definable with parameters’.)
. (We point out that ‘definable’ will always mean ‘definable with parameters’.)
Definition 1.1. Let X ⊆ ℝn. X is called semi-bounded if it is definable in the structure ‹ℝ, +, <, λa, B1, …, Bk›a∈ℝ, where the Bi's are bounded subsets of ℝn.
The main result of this paper (see Theorem 3.1) shows roughly that, in Ominimal expansions of 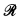 that satisfy the partition condition (see Definition 2.3), every semibounded set can be partitioned into finitely many sets, each of which is of a form similar to a cylinder. Namely, these sets are obtained through the “stretching” of a bounded cell by finitely many linear vectors. As a corollary (see Theorem 1.4), we get different characterizations of semibounded sets, either in terms of their structure or in terms of their definability power.
that satisfy the partition condition (see Definition 2.3), every semibounded set can be partitioned into finitely many sets, each of which is of a form similar to a cylinder. Namely, these sets are obtained through the “stretching” of a bounded cell by finitely many linear vectors. As a corollary (see Theorem 1.4), we get different characterizations of semibounded sets, either in terms of their structure or in terms of their definability power.
The following result, by A. Pillay, P. Scowcroft and C. Steinhorn, was the main motivation for this paper. The theorem is formulated here in a slightly stronger form than originally, but the proof itself is essentially the original one. A short version of the proof is included in §4.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 15
- Cited by

