Published online by Cambridge University Press: 12 March 2014
Let M be an L-structure and A be an infinite subset of M. Two structures can be defined from A:
• The induced structure on A has a name Rφ for every ∅-definable relation φ(M) ∩ An on A. Its language is
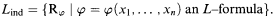
A with its Lind-structure will be denoted by Aind.
• The pair (M, A) is an L(P)-structure, where P is a unary predicate for A and L(P) = L ∪{P}.
We call A small if there is a pair (N, B) elementarily equivalent to (M, A) and such that for every finite subset b of N every L–type over Bb is realized in N.
A formula φ(x, y) has the finite cover property (f.c.p) in M if for all natural numbers k there is a set of φ–formulas
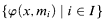
which is k–consistent but not consistent in M. M has the f.c.p if some formula has the f.c.p in M. It is well known that unstable structures have the f.c.p. (see [6].) We will prove the following two theorems.
Theorem A. Let A be a small subset of M. If M does not have the finite cover property then, for every λ ≥ ∣L∣, if both M andAindare λ–stable then (M, A) is λ–stable.
Corollary 1.1 (Poizat [5]). If M does not have the finite cover property and N ≺ M is a small elementary substructure, then (M, N) is stable.
Corollary 1.2 (Zilber [7]). If U is the group of wots of unity in the field ℂ of complex numbers the pair (ℂ, U) isω–stable.
Proof. (See [4].) As a strongly minimal set ℂ is ω–stable and does not have the f.c.p. By the subspace theorem of Schmidt [3] every algebraic set intersects U in a finite union of translates of subgroups definable in the group structure of U alone. Whence Uind is nothing more than a (divisible) abelian group, which is ω–stable.