Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Laskowski, M.C.
and
Terry, C.A.
2022.
Jumps in speeds of hereditary properties in finite relational languages.
Journal of Combinatorial Theory, Series B,
Vol. 154,
Issue. ,
p.
93.
BRAUNFELD, SAMUEL
and
LASKOWSKI, MICHAEL C.
2022.
COUNTING SIBLINGS IN UNIVERSAL THEORIES.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 3,
p.
1130.
Braunfeld, Samuel
and
Laskowski, Michael C.
2022.
Mutual algebraicity and cellularity.
Archive for Mathematical Logic,
Vol. 61,
Issue. 5-6,
p.
841.

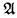 in a finite, relational language has fewer than 2
in a finite, relational language has fewer than 2