Article contents
SQUARES AND NARROW SYSTEMS
Published online by Cambridge University Press: 08 September 2017
Abstract
A narrow system is a combinatorial object introduced by Magidor and Shelah in connection with work on the tree property at successors of singular cardinals. In analogy to the tree property, a cardinal κ satisfies the narrow system property if every narrow system of height κ has a cofinal branch. In this paper, we study connections between the narrow system property, square principles, and forcing axioms. We prove, assuming large cardinals, both that it is consistent that ℵω+1 satisfies the narrow system property and 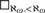 $\square _{\aleph _\omega, < \aleph _\omega } $ holds and that it is consistent that every regular cardinal satisfies the narrow system property. We introduce natural strengthenings of classical square principles and show how they can be used to produce narrow systems with no cofinal branch. Finally, we show that the Proper Forcing Axiom implies that every narrow system of countable width has a cofinal branch but is consistent with the existence of a narrow system of width ω1 with no cofinal branch.
$\square _{\aleph _\omega, < \aleph _\omega } $ holds and that it is consistent that every regular cardinal satisfies the narrow system property. We introduce natural strengthenings of classical square principles and show how they can be used to produce narrow systems with no cofinal branch. Finally, we show that the Proper Forcing Axiom implies that every narrow system of countable width has a cofinal branch but is consistent with the existence of a narrow system of width ω1 with no cofinal branch.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 9
- Cited by

