Article contents
Some results in polychromatic Ramsey theory
Published online by Cambridge University Press: 12 March 2014
Extract
Classical Ramsey theory (at least in its simplest form) is concerned with problems of the following kind: given a set X and a colouring of the set [X]n of unordered n-tuples from X, find a subset Y ⊆ X such that all elements of [Y]n get the same colour. Subsets with this property are called monochromatic or homogeneous, and a typical positive result in Ramsey theory has the form that when X is large enough and the number of colours is small enough we can expect to find reasonably large monochromatic sets.
Polychromatic Ramsey theory is concerned with a “dual” problem, in which we are given a colouring of [X]n and are looking for subsets Y ⊆ X such that any two distinct elements of [Y]n get different colours. Subsets with this property are called polychromatic or rainbow. Naturally if we are looking for rainbow subsets then our task becomes easier when there are many colours. In particular given an integer k we say that a colouring is k-bounded when each colour is used for at most k many n-tuples.
At this point it will be convenient to introduce a compact notation for stating results in polychromatic Ramsey theory. We recall that in classical Ramsey theory we write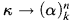 to mean “every colouring of [κ]n in k colours has a monochromatic set of order type α”. We will write
to mean “every colouring of [κ]n in k colours has a monochromatic set of order type α”. We will write 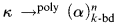 to mean “every k-bounded colouring of [κ]n has a polychromatic set of order type α”. We note that when κ is infinite and k is finite a k-bounded colouring will use exactly κ colours, so we may as well assume that κ is the set of colours used.
to mean “every k-bounded colouring of [κ]n has a polychromatic set of order type α”. We note that when κ is infinite and k is finite a k-bounded colouring will use exactly κ colours, so we may as well assume that κ is the set of colours used.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
- 3
- Cited by

