Article contents
Some results concerning strongly compact cardinals
Published online by Cambridge University Press: 12 March 2014
Extract
This paper consists of two parts. In §1 we mention the first strongly compact cardinal. Magidor proved in [6] that it can be the first measurable and it can be also the first supercompact. In [2], Apter proved that Con(ZFC + there is a supercompact limit of supercompact cardinals) implies Con(ZFC + the first strongly compact cardinal κ is ϕ(κ)-supercompact + no α < κ is ϕ(α)-supercompact) for a formula ϕ which satisfies certain conditions.
We shall get almost the same conclusion as Apter's theorem assuming only one supercompact cardinal. Our notion of forcing is the same as in [2] and a trick makes it possible.
In §2 we study a kind of fine ultrafilter on Pκλ investigated by Menas in [7], where κ is a measurable limit of strongly compact cardinals. He showed that such an ultrafilter is not normal in some case (Theorems 2.21 and 2.22 in [7]). We shall show that it is not normal in any case (even if κ is supercompact). We also prove that it is weakly normal in some case.
We work in ZFC and much of our notation is standard. But we mention the following: the letters α,β,γ… denote ordinals, whereas κ,λ,μ,… are reserved for cardinals. R(α) is the collection of sets rank <α. φM denotes the realization of a formula φ to a class M. Except when it is necessary, we drop “M”. For example, M ⊩ “κ is φ(κ)-supercompact” means “κ is φM(κ)-supercompact in M”. If x is a set, |x| is its cardinality, Px is its power set, and 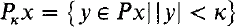 . If also x ⊆ OR,
. If also x ⊆ OR, 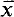 denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “p < q” means “p is stronger than q”.
denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “p < q” means “p is stronger than q”.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 1
- Cited by

