Hostname: page-component-cb9f654ff-pvkqz Total loading time: 0 Render date: 2025-08-14T14:01:24.150Z Has data issue: false hasContentIssue false
  • English
  • Français

SHORTENING CLOPEN GAMES

Part of: Set theory Game theory Classical measure theory

Published online by Cambridge University Press:  08 January 2021

JUAN P. AGUILERA
JUAN P. AGUILERA*
Affiliation:
DEPARTMENT OF MATHEMATICS GHENT UNIVERSITY KRIJGSLAAN 281-S8, 9000 GHENT, BELGIUM and INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY VIENNA UNIVERSITY OF TECHNOLOGY WIEDNER HAUPTSTRASSE 8–10, 1040 VIENNA, AUSTRIA E-mail: aguilera@logic.at
Get access Rights & Permissions [Opens in a new window]

Abstract

For every countable wellordering 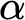$\alpha $ greater than 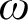$\omega $, it is shown that clopen determinacy for games of length 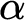$\alpha $ with moves in 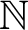$\mathbb {N}$ is equivalent to determinacy for a class of shorter games, but with more complicated payoff. In particular, it is shown that clopen determinacy for games of length 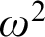$\omega ^2$ is equivalent to 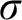$\sigma $-projective determinacy for games of length 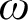$\omega $ and that clopen determinacy for games of length 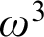$\omega ^3$ is equivalent to determinacy for games of length 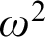$\omega ^2$ in the smallest 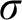$\sigma $-algebra on 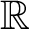$\mathbb {R}$ containing all open sets and closed under the real game quantifier.

Keywords

determinacyclopen gameinfinite gamelong gameσ-algebra

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 03E60: Determinacy principles 28A05: Classes of sets (Borel fields, $sigma$-rings, etc.), measurable sets, Suslin sets, analytic sets 91A44: Games involving topology or set theory

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1541 - 1554
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aguilera, J. P., $\sigma$ -Projective determinacy, to appear, 2018.Google Scholar
Aguilera, J. P., Between the finite and the infinite, Ph.D. thesis, Vienna University of Technology, 2019.Google Scholar
Aguilera, J. P., Müller, S., and Schlicht, P., Long games and $\sigma$ -projective sets. Annals of Pure and Applied Logic, vol. 172 (2021).10.1016/j.apal.2020.102939CrossRefGoogle Scholar
Blass, A., Equivalence of two strong forms of determinacy. Proceedings of the American Mathematical Society, vol. 52 (1975), pp. 373–376.10.1090/S0002-9939-1975-0373903-XCrossRefGoogle Scholar
Gale, D. and Stewart, F. M., Infinite games with perfect information, Contributions to the Theory of Games , vol. 2 (H. W. Kuhn and A. W. Tucker, editors), Princeton University Press, Princeton, 1953, pp. 245–266.Google Scholar
Harrington, L., Analytic determinacy and 0# , this Journal, vol. 43 (1978), pp. 685–693.Google Scholar
Martin, D. A., Borel determinacy . Annals of Mathematics, vol. 102 (1975), no. 2, pp. 363–371.CrossRefGoogle Scholar
Martin, D. A., Determinacy of infinitely long games, Book draft dated March 2020.Google Scholar
Moschovakis, Y. N., Elementary Induction on Abstract Structures, Studies in Logic and the Foundations of Mathematics, Elsevier, Amsterdam, 1974.Google Scholar
Moschovakis, Y. N., Descriptive Set Theory, second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.10.1090/surv/155CrossRefGoogle Scholar
Trang, N. D., Generalized Solovay measures, the HOD analysis, and the core model induction, Ph.D. thesis, University of California at Berkeley, 2013.Google Scholar
Welch, P. D., Determinacy in strong cardinal models , this Journal, vol. 76 (2011), pp. 719–728.Google Scholar