Published online by Cambridge University Press: 12 March 2014
Let M be an o-minimal structure or a p-adically closed field. Let 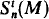 be the space of complete n-types over M equipped with the following topology: The basic open sets of
be the space of complete n-types over M equipped with the following topology: The basic open sets of 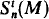 are of the form Ũ = {p ∈ Sn (M): U ∈ p} for U an open definable subset of Mn .
are of the form Ũ = {p ∈ Sn (M): U ∈ p} for U an open definable subset of Mn . 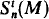 is a spectral space. (For M = K a real closed field,
is a spectral space. (For M = K a real closed field, 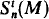 is precisely the real spectrum of K[X 1, …, Xn ]; see [CR].) We will equip
is precisely the real spectrum of K[X 1, …, Xn ]; see [CR].) We will equip 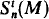 with a sheaf of LM -structures (where LM is a suitable language). Again for M a real closed field this corresponds to the structure sheaf on
with a sheaf of LM -structures (where LM is a suitable language). Again for M a real closed field this corresponds to the structure sheaf on 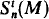 (see [S]). Our main point is that when Th(M) has definable Skolem functions, then if p ∈
(see [S]). Our main point is that when Th(M) has definable Skolem functions, then if p ∈ 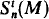 , it follows that M(p), the definable ultrapower of M at p, can be factored through Mp , the stalk at p with respect to the above sheaf. This depends on the observation that if M ≺ N, a ∈ Nn and f is an M-definable (partial) function defined at a, then there is an open M-definable set U ⊂ Nn with a ∈ U, and a continuous M-definable function g:U → N such that g(a) = f(a).
, it follows that M(p), the definable ultrapower of M at p, can be factored through Mp , the stalk at p with respect to the above sheaf. This depends on the observation that if M ≺ N, a ∈ Nn and f is an M-definable (partial) function defined at a, then there is an open M-definable set U ⊂ Nn with a ∈ U, and a continuous M-definable function g:U → N such that g(a) = f(a).
In the case that M is an o-minimal expansion of a real closed field (or M is a p-adically closed field), it turns out that M(p) can be recovered as the unique quotient of Mp which is an elementary extension of M.