Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ghilardi, Silvio
1995.
An algebraic theory of normal forms.
Annals of Pure and Applied Logic,
Vol. 71,
Issue. 3,
p.
189.
Visser, Albert
1996.
Gödel ’96.
Vol. 6,
Issue. ,
p.
139.
Polacik, Tomasz
1997.
Computational Logic and Proof Theory.
Vol. 1289,
Issue. ,
p.
255.
Ghilardi, Silvio
and
Zawadowski, Marek
1997.
Model completions and r-Heyting categories.
Annals of Pure and Applied Logic,
Vol. 88,
Issue. 1,
p.
27.
Połacik, Tomasz
1998.
Pitts' Quantifiers Are Not Topological Quantification.
Notre Dame Journal of Formal Logic,
Vol. 39,
Issue. 4,
Visser, Albert
1999.
Rules and Arithmetics.
Notre Dame Journal of Formal Logic,
Vol. 40,
Issue. 1,
Janin, D.
and
Lenzi, G.
2001.
Relating levels of the mu-calculus hierarchy and levels of the monadic hierarchy.
p.
347.
Visser, Albert
2002.
Substitutions of Σ10-sentences: explorations between intuitionistic propositional logic and intuitionistic arithmetic.
Annals of Pure and Applied Logic,
Vol. 114,
Issue. 1-3,
p.
227.
French, Tim
2005.
FSTTCS 2005: Foundations of Software Technology and Theoretical Computer Science.
Vol. 3821,
Issue. ,
p.
396.
Artemov, Sergei N.
and
Beklemishev, Lev D.
2005.
Handbook of Philosophical Logic, 2nd Edition.
Vol. 13,
Issue. ,
p.
189.
D’Agostino, Giovanna
and
Lenzi, Giacomo
2005.
An axiomatization of bisimulation quantifiers via the μ-calculus.
Theoretical Computer Science,
Vol. 338,
Issue. 1-3,
p.
64.
Visser, Albert
2005.
Processes, Terms and Cycles: Steps on the Road to Infinity.
Vol. 3838,
Issue. ,
p.
14.
D'Agostino, G.
and
Lenzi, G.
2006.
On modal μ-calculus with explicit interpolants.
Journal of Applied Logic,
Vol. 4,
Issue. 3,
p.
256.
Bílková, Marta
2007.
Uniform Interpolation and Propositional Quantifiers in Modal Logics.
Studia Logica,
Vol. 85,
Issue. 1,
p.
1.
O’Connor, Michael
2007.
Logical Foundations of Computer Science.
Vol. 4514,
Issue. ,
p.
437.
Aguzzoli, Stefano
Gerla, Brunella
and
Marra, Vincenzo
2008.
Gödel algebras free over finite distributive lattices.
Annals of Pure and Applied Logic,
Vol. 155,
Issue. 3,
p.
183.
Shamkanov, Daniyar S.
2011.
Interpolation properties for provability logics GL and GLP.
Proceedings of the Steklov Institute of Mathematics,
Vol. 274,
Issue. 1,
p.
303.
Bezhanishvili, Nick
and
de Jongh, Dick
2012.
Extendible Formulas in Two Variables in Intuitionistic Logic.
Studia Logica,
Vol. 100,
Issue. 1-2,
p.
61.
ALIZADEH, MAJID
DERAKHSHAN, FARZANEH
and
ONO, HIROAKIRA
2014.
UNIFORM INTERPOLATION IN SUBSTRUCTURAL LOGICS.
The Review of Symbolic Logic,
Vol. 7,
Issue. 3,
p.
455.
Maksimova, L. L.
2014.
The Lyndon property and uniform interpolation over the Grzegorczyk logic.
Siberian Mathematical Journal,
Vol. 55,
Issue. 1,
p.
118.
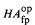 is a bi-Heyting category satisfying the Lawvere condition. We show that the embedding Φ:
is a bi-Heyting category satisfying the Lawvere condition. We show that the embedding Φ: 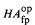 → Sh(P0, J0) into the topos of sheaves, (P0 is the category of finite rooted posets and open maps, J0 the canonical topology on P0) given by H ↦ HA(H,
→ Sh(P0, J0) into the topos of sheaves, (P0 is the category of finite rooted posets and open maps, J0 the canonical topology on P0) given by H ↦ HA(H, 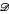 (−)) : P0 → Set preserves the structure mentioned above, finite coproducts, and subobject classifier; it is also conservative. This whole structure on
(−)) : P0 → Set preserves the structure mentioned above, finite coproducts, and subobject classifier; it is also conservative. This whole structure on 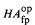 can be derived from that of Sh(P0, J0) via the embedding Φ. We also show that the equivalence relations in
can be derived from that of Sh(P0, J0) via the embedding Φ. We also show that the equivalence relations in 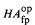 are not effective in general. On the way to these results we establish a new kind of duality between
are not effective in general. On the way to these results we establish a new kind of duality between 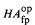 and a category of sheaves equipped with certain structure defined in terms of Ehrenfeucht games. Our methods are model-theoretic and combinatorial as opposed to proof-theoretic as in [Pi].
and a category of sheaves equipped with certain structure defined in terms of Ehrenfeucht games. Our methods are model-theoretic and combinatorial as opposed to proof-theoretic as in [Pi].
