No CrossRef data available.
Article contents
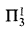 sets and
sets and 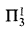 singletons
singletons
Published online by Cambridge University Press: 12 March 2014
Abstract
We extend work of H. Friedman, L. Harrington and P. Welch to the third level of the projective hierarchy. Our main theorems say that (under appropriate background assumptions) the possibility to select definable elements of non-empty sets of reals at the third level of the projective hierarchy is equivalent to the disjunction of determinacy of games at the second level of the projective hierarchy and the existence of a core model (corresponding to this fragment of determinacy) which must then contain all real numbers. The proofs use Sacks forcing with perfect trees and core model techniques.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999
References
REFERENCES
[1]
Dodd, A. J., The core model, London Mathematical Society Lecture Note Series, no. 61, 1984, xxxviii + 229 pp.Google Scholar
[3]
Gödel, K., The consistency of the axiom of choice and the generalized continuum hypothesis, Proceedings of the National Academy of Sciences of the USA, vol. 24 (1938), pp. 556–557.CrossRefGoogle ScholarPubMed
[4]
Gödel, K., The consistency of the axiom of choice and of the generalized continuum hypothesis with the axioms of set theory, Annals of Mathematical Studies, Study 3, Princeton University Press, Princeton, New Jersey, 1940.Google Scholar
[5]
Harrington, L.,
 sets and
sets and  singletons, American Mathematical Society, vol. 52 (1975), pp. 356–360.Google Scholar
singletons, American Mathematical Society, vol. 52 (1975), pp. 356–360.Google Scholar
[6]
Hauser, K., Sets of reals, infinite games and core model theory, Proceedings of the 6th Asian Logic Conference, Beijing 1996, World Scientific Publishing Co., Singapore, 1998, pp. 107–120.Google Scholar
[8]
Kondo, M., Sur l'uniformization des complementaires analytiques et les ensembles projectifs de la second classe, Japanese Journal of Mathematics, vol. 15 (1938), pp. 197–230.Google Scholar
[10]
Mansfield, R., The nonexistence of  wellorderings of the Baire space, Fundamenta Mathematical, vol. 86 (1975), pp. 279–281.Google Scholar
wellorderings of the Baire space, Fundamenta Mathematical, vol. 86 (1975), pp. 279–281.Google Scholar
[11]
Martin, D. A. and Solovay, R. M., A basis theorem for  sets of reals, Annals of Mathematics, vol. 89 (1969), pp. 138–160.CrossRefGoogle Scholar
sets of reals, Annals of Mathematics, vol. 89 (1969), pp. 138–160.CrossRefGoogle Scholar
[12]
Martin, D. A. and Steel, J. R., Iteration trees, Journal of the American Mathematical Society, vol. 7 (1994), pp. 1–73.CrossRefGoogle Scholar
[13]
Mitchell, W. J. and Steel, J. R., Fine structure and iteration trees, Lecture Notes in Logic, no. 3, Springer-Verlag, 1994, 130 pp.CrossRefGoogle Scholar
[15]
Sacks, G., Forcing with perfect closed sets, Axiomatic set theory (Scott, D., editor), vol. 13, Proceedings of Symposia in Pure Mathematics, no. II, American Mathematical Society, Providence, Rhode Island, 1971, pp. 331–355.Google Scholar
[16]
Shoenfield, J., The problem of predicativity, Essays on the foundation of mathematics (Bar-Hillel, Y.
et al., editors), The Magnes Press, Jerusalem, 1961, pp. 132–142.Google Scholar
[17]
Steel, J. R., The core model iterability problem, Lecture Notes in Logic, no. 8. Springer-Verlag, 1996, 112 pp.CrossRefGoogle Scholar
[18]
Welch, P., Some descriptive set theory and core models, Annals of Pure and Applied Logic, vol. 39 (1989), pp. 273–290.Google Scholar
[19]
Woodin, W. H., Mathias, A. R. D., and Hauser, K., The axiom of determinacy, monograph in preparation.Google Scholar

