Article contents
Scott heights of abelian groups
Published online by Cambridge University Press: 12 March 2014
Extract
The Scott height of a structure gives ordinal measure of the inhomogeneity of the structure. The Scott specturm of a collection of structures is the set of Scott heights of structures in the collection. We will recall the precise definitions of these and related concepts in the next section. The reader thoroughly unfamiliar with these notions may want to skip ahead before reading the rest of this Introduction.
In [11] it is shown that every model of the complete theory of ( , +, 1), where, as usual,
, +, 1), where, as usual,  denotes the integers, is ℵ0-homogeneous, and therefore has Scott height at most ω. On the other hand, a footnote in [1] gives a model of the theory of (
denotes the integers, is ℵ0-homogeneous, and therefore has Scott height at most ω. On the other hand, a footnote in [1] gives a model of the theory of ( , +) which is not ℵ0-homogeneous, while in [11] such a model is described which can be expanded to a model of the theory of (
, +) which is not ℵ0-homogeneous, while in [11] such a model is described which can be expanded to a model of the theory of ( , +, 1). However, since it is also true that any model of the theory of (
, +, 1). However, since it is also true that any model of the theory of ( , +) is isomorphic to a subgroup, in fact a pure subgroup, of a direct sum of
, +) is isomorphic to a subgroup, in fact a pure subgroup, of a direct sum of 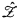 and a torsion-free divisible group, it is easy to see that any such model must be ≡∞ω to a model of cardinality at most
and a torsion-free divisible group, it is easy to see that any such model must be ≡∞ω to a model of cardinality at most 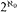 and so must have Scott height below
and so must have Scott height below 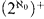 .
.
After having recalled the relevant material about Scott heights in §2, we will review the situation for torsion abelian groups in §3. In §4 we shall produce torsion-free abelian groups of high Scott height. It is the proof of Theorem 15 that was our primary motivation in writing this paper.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994
References
REFERENCES
- 3
- Cited by

