Article contents
Rothberger's property and partition relations
Published online by Cambridge University Press: 12 March 2014
Extract
Let X be an infinite but separable metric space. An open cover 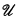 of X is said to be large if for each x ϵ X the set {U ϵ
of X is said to be large if for each x ϵ X the set {U ϵ 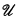 : x ϵ U} is infinite. The symbol Λ denotes the collection of large open covers of X. An open cover
: x ϵ U} is infinite. The symbol Λ denotes the collection of large open covers of X. An open cover 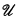 of X is said to be an ω-cover if for each finite subset F of X there is a U ϵ
of X is said to be an ω-cover if for each finite subset F of X there is a U ϵ 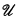 such that F ⊆ U, and X is not a member of
such that F ⊆ U, and X is not a member of 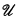 , X is said to have Rothberger's property if there is for every sequence (
, X is said to have Rothberger's property if there is for every sequence (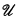 n : n = 1,2,3,…) of open covers of X a sequence (Un : n = 1,2,3,…) such that:
n : n = 1,2,3,…) of open covers of X a sequence (Un : n = 1,2,3,…) such that:
(1) for each n, Un is a member of 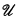 n, and
n, and
(2) {Un: n = 1,2,3,…} is a cover of X.
Rothberger introduced this property in his paper [2]. For convenience we let 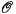 denote the collection of all open covers of X.
denote the collection of all open covers of X.
In [3] it was shown that X has Rothberger's property if, and only if, the following partition relation is true for large open covers of X:
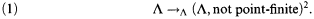
This partition relation means:
for every large cover 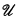 of X, for every coloring
of X, for every coloring
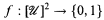
such that for each U ϵ 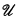 and each large cover
and each large cover 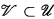 there is an i with
there is an i with 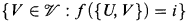 a large cover of X,
a large cover of X,
either there is a large cover 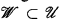 such that f({A, B}) = 0 whenever {A,B} ϵ
such that f({A, B}) = 0 whenever {A,B} ϵ 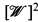 ,
,
or else there is a 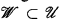 which is not point–finite such that f{{A, B}) = 1 whenever {A, B} ϵ
which is not point–finite such that f{{A, B}) = 1 whenever {A, B} ϵ 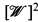 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 1
- Cited by

