Published online by Cambridge University Press: 17 April 2014
Let 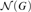 ${\cal N}\left( G \right)$ be the maximal normal definable torsion-free subgroup of a
group G definable in an o-minimal structure M.
We prove that the quotient
${\cal N}\left( G \right)$ be the maximal normal definable torsion-free subgroup of a
group G definable in an o-minimal structure M.
We prove that the quotient 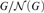 $G/{\cal N}\left( G \right)$ has a maximal definably compact subgroup K,
which is definably connected and unique up to conjugation. Moreover, we show
that K has a definable torsion-free complement, i.e., there is
a definable torsion-free subgroup H such that
$G/{\cal N}\left( G \right)$ has a maximal definably compact subgroup K,
which is definably connected and unique up to conjugation. Moreover, we show
that K has a definable torsion-free complement, i.e., there is
a definable torsion-free subgroup H such that 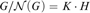 $G/{\cal N}\left( G \right) = K \cdot H$ and
$G/{\cal N}\left( G \right) = K \cdot H$ and 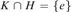 $K\mathop \cap \nolimits^ \,H = \left\{ e \right\}$. It follows that G is definably homeomorphic
to
$K\mathop \cap \nolimits^ \,H = \left\{ e \right\}$. It follows that G is definably homeomorphic
to  $K \times {M^s}$ (with
$K \times {M^s}$ (with 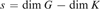 $s = {\rm{dim}}\,G - {\rm{dim}}\,K$), and homotopy equivalent to K. This gives a
(definably) topological reduction to the compact case, in analogy with Lie
groups.
$s = {\rm{dim}}\,G - {\rm{dim}}\,K$), and homotopy equivalent to K. This gives a
(definably) topological reduction to the compact case, in analogy with Lie
groups.