Article contents
PROVABILITY LOGICS RELATIVE TO A FIXED EXTENSION OF PEANO ARITHMETIC
Published online by Cambridge University Press: 23 October 2018
Abstract
Let T and U be any consistent theories of arithmetic. If T is computably enumerable, then the provability predicate 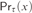 $P{r_\tau }\left( x \right)$ of T is naturally obtained from each
$P{r_\tau }\left( x \right)$ of T is naturally obtained from each 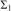 ${{\rm{\Sigma }}_1}$ definition
${{\rm{\Sigma }}_1}$ definition 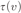 $\tau \left( v \right)$ of T. The provability logic
$\tau \left( v \right)$ of T. The provability logic 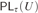 $P{L_\tau }\left( U \right)$ of τ relative to U is the set of all modal formulas which are provable in U under all arithmetical interpretations where □ is interpreted by
$P{L_\tau }\left( U \right)$ of τ relative to U is the set of all modal formulas which are provable in U under all arithmetical interpretations where □ is interpreted by 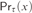 $P{r_\tau }\left( x \right)$. It was proved by Beklemishev based on the previous studies by Artemov, Visser, and Japaridze that every
$P{r_\tau }\left( x \right)$. It was proved by Beklemishev based on the previous studies by Artemov, Visser, and Japaridze that every 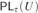 $P{L_\tau }\left( U \right)$ coincides with one of the logics
$P{L_\tau }\left( U \right)$ coincides with one of the logics 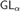 $G{L_\alpha }$,
$G{L_\alpha }$, 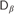 ${D_\beta }$,
${D_\beta }$, 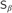 ${S_\beta }$, and
${S_\beta }$, and 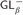 $GL_\beta ^ -$, where α and β are subsets of ω and β is cofinite.
$GL_\beta ^ -$, where α and β are subsets of ω and β is cofinite.
We prove that if U is a computably enumerable consistent extension of Peano Arithmetic and L is one of 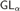 $G{L_\alpha }$,
$G{L_\alpha }$, 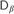 ${D_\beta }$,
${D_\beta }$, 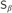 ${S_\beta }$, and
${S_\beta }$, and 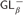 $GL_\beta ^ -$, where α is computably enumerable and β is cofinite, then there exists a
$GL_\beta ^ -$, where α is computably enumerable and β is cofinite, then there exists a 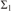 ${{\rm{\Sigma }}_1}$ definition
${{\rm{\Sigma }}_1}$ definition 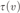 $\tau \left( v \right)$ of some extension of
$\tau \left( v \right)$ of some extension of  $I{{\rm{\Sigma }}_1}$ such that
$I{{\rm{\Sigma }}_1}$ such that 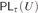 $P{L_\tau }\left( U \right)$ is exactly L.
$P{L_\tau }\left( U \right)$ is exactly L.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 4
- Cited by

