Article contents
Provability in finite subtheories of PA and relative interpretability: a modal investigation
Published online by Cambridge University Press: 12 March 2014
Extract
By Solovay's theorem [16], the modal logic of provability GL gives a complete description of the propositional schemata involving the provability predicate PrPA(x) for Peano arithmetic PA, which are provable in PA. However, many important aspects of provability cannot be fully expressed in terms of PrPA(x). For this reason, many authors have introduced extensions of GL which take account either of Rosser constructions or of other important metamathematical formulas (see, for example, [5], [6], [14], [16], and [19]). In this paper, we concentrate on the modal logic of the provability predicate for finitely axiomatizable subtheories of PA; the interest of this modal logic is based on the following facts. First of all, it provides a modal translation of a very important property of PA, namely the essential reflexiveness. Secondly, in view of Orey's theorem [10] it constitutes a possible approach to the study of interpretability of finite extensions of PA. Indeed, by Orey's theorem PA + θ is interpretable in PA + θ′ iff 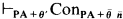 for every n, and, therefore, relative interpretability of finitely axiomatizable extensions of PA can be expressed by means of the provability predicate for finitely axiomatizable subtheories of PA.
for every n, and, therefore, relative interpretability of finitely axiomatizable extensions of PA can be expressed by means of the provability predicate for finitely axiomatizable subtheories of PA.
In §1, we introduce three modal logics extending GL and discuss their arithmetical interpretations; §2 deals with Kripke semantics for two of these logics. In §3, a theorem on arithmetical completeness is shown, which characterizes the logic of the provability predicate for finitely axiomatizable subtheories of PA; a uniform version of this theorem is proved in §4.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
REFERENCES
- 12
- Cited by

