Article contents
A polynomial translation of S4 into intuitionistic logic
Published online by Cambridge University Press: 12 March 2014
Extract
It is known that both S4 and the Intuitionistic prepositional calculus Int are P-SPACE complete. This guarantees that there is a polynomial translation from each system into the other.
However, no sound and faithful polynomial translation from S4 into Int is commonly known. The problem of finding one was suggested by Dana Scott during a very informal gathering of logicians in February 2005 at UCLA. Grigori Mints then brought it to my attention, and in this paper I present a solution. It is based on Kripke semantics and describes model-checking for S4 using formulas of Int.
A simple translation from Int into S4, the Gödel-Tarski translation, is wellknown; given a formula φ of Int, one obtains 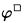 by prefixing □ to every subformula. For example,
by prefixing □ to every subformula. For example,
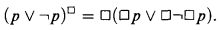 .
.
That the translation is sound and faithful can be seen by considering topological semantics, which assign open sets both to □-formulas of S4 and arbitrary formulas of Int; the interpretation of φ and 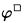 turn out to be identical. See Tarski's paper [6] for details. Gödel's original paper can be found in [3].
turn out to be identical. See Tarski's paper [6] for details. Gödel's original paper can be found in [3].
In [2], Friedman and Flagg present a kind of inverse to Gödel-Tarski. Given a formula φ of S4 and a finite set of formulas Γ of Int, for each ε ∈ Γ one gets an intuitionistic formula 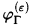 given recursively by
given recursively by
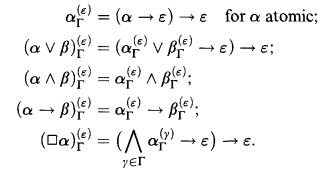
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006
References
REFERENCES
- 5
- Cited by

