Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-30T06:26:22.480Z Has data issue: false hasContentIssue false
  • English
  • Français

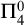$\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM

Part of: Proof theory and constructive mathematics Extremal combinatorics Nonstandard models General logic

Published online by Cambridge University Press:  27 January 2025

QUENTIN LE HOUÉROU  and
LUDOVIC LEVY PATEY Open the ORCID record for LUDOVIC LEVY PATEY [Opens in a new window]
QUENTIN LE HOUÉROU
Affiliation:
LABORATOIRE D’ALGORITHMIQUE COMPLEXITÉ ET LOGIQUE UNIVERSITÉ PARIS-EST-CRÉTEIL-VAL-DE-MARNE, CRÉTEIL, FRANCE E-mail: quentin.le-houerou@computability.fr
LUDOVIC LEVY PATEY*
Affiliation:
CNRS, ÉQUIPE DE LOGIQUE, INSTITUT DE MATHÉMATIQUES DE JUSSIEU-PARIS RIVE GAUCHE UNIVERSITÉ PARIS CITÉ - CAMPUS DES GRANDS MOULINS, PARIS, FRANCE
*
E-mail: ludovic.patey@computability.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

A left-variable word over an alphabet A is a word over 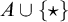$A \cup \{\star \}$ whose first letter is the distinguished symbol $\star $ standing for a placeholder. The ordered variable word theorem (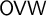$\mathsf {OVW}$), also known as Carlson–Simpson’s theorem, is a tree partition theorem, stating that for every finite alphabet A and every finite coloring of the words over A, there exists a word 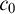$c_0$ and an infinite sequence of left-variable words 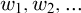$w_1, w_2, \dots $ such that 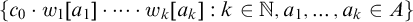$\{ c_0 \cdot w_1[a_1] \cdot \dots \cdot w_k[a_k] : k \in \mathbb {N}, a_1, \dots , a_k \in A \}$ is monochromatic.

In this article, we prove that $\mathsf {OVW}$ is 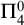$\Pi ^0_4$-conservative over 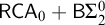$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_2$. This implies in particular that $\mathsf {OVW}$ does not imply $\mathsf {ACA}_0$ over $\mathsf {RCA}_0$. This is the first principle for which the only known separation from $\mathsf {ACA}_0$ involves non-standard models.

Keywords

Ramsey theoryfirst-order arithmeticreverse mathematicsconservationweak arithmetic

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics) 03F35: Second- and higher-order arithmetic and fragments
Secondary: 03H15: Nonstandard models of arithmetic 05D10: Ramsey theory
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 16
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

d’Auriac, P.-E. A., Liu, L., Mignoty, B., and Patey, L., Carlson-Simpson’s lemma and applications in reverse mathematics . Annals of Pure and Applied Logic , vol. 174 (2023), no. 9, p. 103287, 16 pp.Google Scholar
d’Auriac, P.-E. A., Cholak, P. A., Dzhafarov, D. D., Monin, B.Ît, and Patey, L., Milliken’s tree theorem and its applications: a computability-theoretic perspective, Memoirs of the AMS, 293 (2024), no. 1457, pp. vi+118.Google Scholar
Carlson, T. J. and Simpson, S. G., A dual form of Ramsey’s theorem . Advances in Mathematics , vol. 53 (1984), no. 3, pp. 265–290.CrossRefGoogle Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for Pairs . The Journal of Symbolic Logic , vol. 66 (2001), no. 1, pp. 1–55.CrossRefGoogle Scholar
Chong, C. T., Li, W., Wang, W., and Yang, Y., On the strength of Ramsey’s theorem for trees . Advances in Mathematics , vol. 369 (2020), p. 107180, 39.CrossRefGoogle Scholar
Chong, C. T., Li, W., Wang, W., and Yang, Y., Conservation strength of the infinite pigeonhole principle for trees . Israel Journal of Mathematics , vol. 260 (2023), pp. 1–24.Google Scholar
Chubb, J., Hirst, J. L., and McNicholl, T. H., Reverse mathematics, computability, and partitions of trees . The Journal of Symbolic Logic , vol. 74 (2009), no. 1, pp. 201–215.CrossRefGoogle Scholar
Corduan, J., Groszek, M. J., and Mileti, J. R., Reverse mathematics and Ramsey’s property for trees . The Journal of Symbolic Logic , vol. 75 (2010), no. 3, pp. 945–954.CrossRefGoogle Scholar
Devlin, D. C., Some partition theorems and ultrafilters on omega, ProQuest LLC, Ann Arbor, MI , Ph.D. thesis, Dartmouth College, 1980.Google Scholar
Dodos, P. and Kanellopoulos, V., Ramsey theory for product spaces , Mathematical Surveys and Monographs, 212, American Mathematical Society, Providence, 2016.CrossRefGoogle Scholar
Dodos, P., Kanellopoulos, V., and Tyros, K., A density version of the Carlson-Simpson theorem . Journal of European Mathematical Society , vol. 16 (2014), no. 10, pp. 2097–2164.CrossRefGoogle Scholar
Dzhafarov, D. D. and Mummert, C., Reverse Mathematics—Problems, Reductions, and Proofs , Theory and Applications of Computability, Springer, Cham, 2022.CrossRefGoogle Scholar
Dzhafarov, D. D. and Patey, L., Coloring trees in reverse mathematics . Advances in Mathematics , vol. 318 (2017), pp. 497–514.CrossRefGoogle Scholar
Fiori-Carones, M., Kołodziejczyk, L. A., Wong, T. L., and Yokoyama, K., An isomorphism theorem for models of weak König’s lemma without primitive recursion. J. Eur. Math. Soc. (2024), published online first.CrossRefGoogle Scholar
Friedman, H., Personal Communication to L , Harrington, Honolulu, HI, 1977.Google Scholar
Friedman, H. and Simpson, S. G., Issues and problems in reverse mathematics , Computability Theory and its Applications (Boulder, CO, 1999) , Contemporary Mathematics, 257, American Mathematical Society, Providence, 2000, pp. 127–144.CrossRefGoogle Scholar
Graham, R. L., Rothschild, B. L., and Spencer, J. H., Ramsey Theory , Wiley Series in Discrete Mathematics and Optimization, Wiley, Hoboken, NJ, 2013, Paperback edition of the second (1990) edition [MR1044995].Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First Order Arithmetic , Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998, Second printing.Google Scholar
Hales, A. W. and Jewett, R. I., Regularity and positional games . Transactions of American Mathematical Society , vol. 106 (1963), pp. 222–229.CrossRefGoogle Scholar
Hirschfeldt, D. R., Slicing the Truth , Lecture Notes Series. Institute for Mathematical Sciences, National University of Singapore, 28, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2015, On the computable and reverse mathematics of combinatorial principles, Edited and with a foreword by Chitat Chong, Qi Feng, Theodore A. Slaman, W. Hugh Woodin and Yue Yang.Google Scholar
Hubička, J., Big Ramsey degrees using parameter spaces, preprint, 2020, arXiv:2009.00967.Google Scholar
Kaye, R., Models of Peano Arithmetic , Oxford Logic Guides, vol. 15, The Clarendon Press, Oxford University Press, New York, 1991.CrossRefGoogle Scholar
Ketonen, J. and Solovay, R., Rapidly growing Ramsey functions . Annals of Mathematics (2) , vol. 113 (1981), no. 2, pp. 267–314.CrossRefGoogle Scholar
Kirby, L. A. S. and Paris, J. B., Initial segments of models of Peano’s axioms , Set Theory and Hierarchy Theory, V (Proc. Third Conf., Bierutowice, 1976) , Lecture Notes in Mathematics, vol. 619, Springer, Berlin, 1977, pp. 211–226.CrossRefGoogle Scholar
Kołodziejczyk, L. A. and Yokoyama, K., Some upper bounds on ordinal-valued Ramsey numbers for colourings of pairs . Selecta Mathematica , vol. 26 (2020), no. 4, p. 56, 18.CrossRefGoogle Scholar
Le Houérou, Q., Patey, L. L., and Yokoyama, K., ${\pi}_4^0$ conservation of Ramsey’s theorem for pairs, in preparation.Google Scholar
Liu, L., Monin, B., and Patey, L., A computable analysis of variable words theorems . Proceedings of the American Mathematical Society , vol. 147 (2019), no. 2, pp. 823–834.CrossRefGoogle Scholar
Miller, J. S. and Solomon, R., Effectiveness for infinite variable words and the dual Ramsey theorem . Archive for Mathematical Logic , vol. 43 (2004), no. 4, pp. 543–555.CrossRefGoogle Scholar
Milliken, K. R., A Ramsey theorem for trees . Journal of Combinatorial Theory Series A , vol. 26 (1979), no. 3, pp. 215–237.CrossRefGoogle Scholar
Patey, L., The strength of the tree theorem for pairs in reverse mathematics . The Journal of Symbolic Logic , vol. 81 (2016), no. 4, pp. 1481–1499.CrossRefGoogle Scholar
Sauer, N. W., Coloring subgraphs of the Rado graph . Combinatorica , vol. 26 (2006), no. 2, pp. 231–253.CrossRefGoogle Scholar
Shelah, S., Primitive recursive bounds for van der Waerden numbers . Journal of American Mathematical Society , vol. 1 (1988), no. 3, pp. 683–697.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Slaman, T. A.,  ${\varSigma}_n$ -bounding and ${\varDelta}_n$ -induction . Proceedings of the American Mathematical Society , vol. 132 (2004), no. 8, pp. 2449–2456.CrossRefGoogle Scholar