Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Starosolski, Andrzej
2014.
Ordinal ultrafilters versus P-hierarchy.
Open Mathematics,
Vol. 12,
Issue. 1,
Starosolski, Andrzej
2014.
Cascades, order, and ultrafilters.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 10,
p.
1626.
Machura, Michał
and
Starosolski, Andrzej
2015.
How high can Baumgartner’s $${\mathcal{I}}$$ I -ultrafilters lie in the P-hierarchy?.
Archive for Mathematical Logic,
Vol. 54,
Issue. 5-6,
p.
555.
Machura, Michał
and
Starosolski, Andrzej
2020.
Thin ultrafilters and the P-hierarchy of ultrafilters.
Topology and its Applications,
Vol. 281,
Issue. ,
p.
107205.
Dolecki, Szymon
and
Starosolski, Andrzej
2021.
Continuous extension of maps between sequential cascades.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 4,
p.
102928.
STAROSOLSKI, ANDRZEJ
2021.
THE RUDIN–KEISLER ORDERING OF P-POINTS UNDER 𝔟 = 𝔠.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 4,
p.
1691.

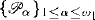 of disjoint classes. We prove that non-emptiness of
of disjoint classes. We prove that non-emptiness of 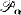 for successor
for successor 