Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-31T00:36:17.772Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthomodularity is not elementary1

Published online by Cambridge University Press:  12 March 2014

Robert Goldblatt
Robert Goldblatt*
Affiliation:
Victoria University Wellington, New Zealand
Get access Rights & Permissions [Opens in a new window]

Extract

In this note it is shown that the property of orthomodularity of the lattice of orthoclosed subspaces of a pre-Hilbert space 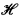is not determined by any first-order properties of the relation ⊥ of orthogonality between vectors in 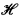. Implications for the study of quantum logic are discussed at the end of the paper.

The key to this result is the following:

If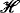is a separable Hilbert space, and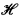is an infinite-dimensional pre-Hilbert subspace of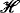, then (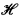, ⊥) and (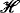, ⊥) are elementarily equivalent in the first-order languageL2of a single binary relation.

Choosing 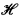to be a pre-Hilbert space whose lattice of orthoclosed subspaces is not orthomodular, we obtain our desired conclusion. In this regard we may note the demonstration by Amemiya and Araki [1] that orthomodularity of the lattice of orthoclosed subspaces is necessary and sufficient for a pre-Hilbert space to be metrically complete, and hence be a Hilbert space. Metric completeness being a notoriously nonelementary property, our result is only to be expected (note also the parallel with the elementary L2-equivalence of the natural order (Q, <) of the rationals and its metric completion to the reals (R, <)).

To derive (1), something stronger is proved, viz. that (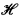, ⊥) is an elementary substructure of (, ⊥).

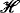Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 401 - 404
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

1

The work reported in this paper was done in late 1975. At the time it presented itself not so much as a contribution to quantum logic as a counterexample to a possible line of enquiry. Recently I explained the results to Bas van Fraassen, who encouraged me to make them available for publication.

References

REFERENCES

[1]Amemiya, I. and Araki, H., A remark on Piron's paper, Publications of the Research Institute of Mathematical Sciences Kyoto University Series A2, vol. 2 (1966), pp. 423–427.CrossRefGoogle Scholar
[2]Bell, J. L. and Slomson, A. B., Models and ultraproducts, North-Holland, Amsterdam, 1969.Google Scholar
[3]Berberian, S. K., Introduction to Hilbert space, Oxford University Press, London, 1961.Google Scholar
[4]Birkhoff, G., Lattice theory, 3rd ed., American Mathematical Society Colloquium Publications, no. 25, American Mathematical Society, Providence, R.I., 1966.Google Scholar
[5]Fine, Kit, Some connections between elementary and modal logic, Proceedings of the Third Scandinavian Logic Symposium (Kanger, Stig, Editor), North-Holland, Amsterdam, 1975, pp. 15–31.CrossRefGoogle Scholar
[6]Goldblatt, R. I., Semantic analysis of orthologic, Journal of Philosophical Logic, vol. 3 (1974), pp. 19–35.CrossRefGoogle Scholar
[7]Halmos, P. R., Introduction to Hilbert space and the theory of spectral multiplicity, Chelsea, New York, 1957.Google Scholar
[8]Lemmon, E. J., An introduction to modal logic, American Philosophical Quarterly Mongraph Series, No. 11, Blackwell, Oxford, 1977.Google Scholar
[9]Maeda, F. and Maeda, S., Theory of symmetric lattices, Springer-Verlag, Berlin and New York, 1970.CrossRefGoogle Scholar
[10]Varadarajan, V. S., Geometry of quantum theory, vol. 1, Van Nostrand, Princeton, N.J., 1968.Google Scholar